Question

f S is circumcentre, G is the centroid, O is the orthocentre of $\vartriangle ABC$ , then $SA + SB + SC$ is equal to?
A). $SG$
B). $OS$
C). $SO$
D). $OG$

Answer 1

Hint: To easily do this type of question firstly take the given points which is given in the question on a line and represent all the points on it then justify which of the lines are making relation with each other from which you can easily do this type of question. As this is a vector based question you must use vector identities as you know in it to easily simplify the answer.

Complete step by step solution: 
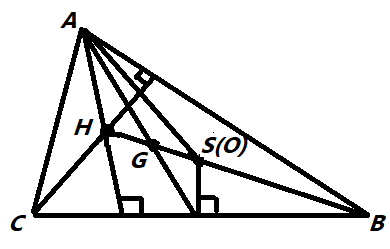
Firstly we can write all the given points which are provided in the question,
Circumcentre = S in $\vartriangle ABC$
Centroid = G in $\vartriangle ABC$
Orthocentre = O in $\vartriangle ABC$
We have to find, $SA + SB + SC$
Let, we assume D is the mid-point of BC
$BD = DC$
As per vector, we know that
$
  DB + DC = 0 \\
    \\
 $ (zero vector or null vector)
By using Plane of Geometry we can say that,
$2SD = AO$
By further simplification we get,
$SA + SB + SC = SA + (SD + DB) + (SD + DC)$
From which by opening brackets and simplifying,
$ = SA + 2SD + (DB + DC)$
In above equation we find that $
  DB + DC = 0 \\
    \\
 $ putting this,
$ = SA + AO + 0$
From which we say that,
$ = SO$
As detail we get that,
 Hence the answer is $SA + SB + SC = SO$ .
Therefore, the correct option is (C)..

Note: In this type of question calculation is very important for everyone as any type of calculation error may reject you from the question because there are many circumstances where you got confused from this you have to be very careful to do this and the identities should be used correctly.