Question

What is the dimensional formula of the moment of force?

Answer 1

Hint: The Moment of a force is a measure of its tendency to cause a body to rotate about a specific point or axis.
The expressions or formulae which tell us how and which of the fundamental quantities are present in a physical quantity are known as the Dimensional Formula of the Physical Quantity.
Theory:
Suppose there is a physical quantity X which depends on base dimensions M (Mass), L (Length), and T (Time) with respective powers a, b and c, then its dimensional formula is represented as: \[\left[ {{M^a}{L^b}{T^c}} \right]\]
Dimensional formula for basic physical quantities,
Mass = $\left[ M \right]$
Distance = \[\left[ L \right]\]
Time =$\left[ T \right]$

Complete solution:
Consider a freely rotating body It rotates about its center.

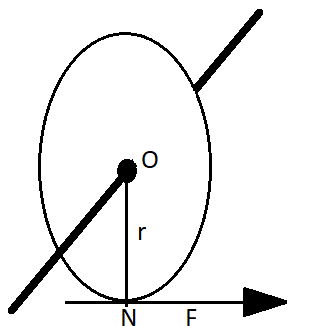
Now when force f is applied the body will start rotating about the fixed point, as long as the line of action of the force passes through O which is a fixed point. This rotating tendency or the turning effect of the force about that point is called the moment of force. We can also say that the moment of the force is the product of the magnitude of the force and the perpendicular distance of the line of action of the force from the axis of rotation.
Moment of a force about point O $ = \left( {F \times ON} \right)$
Here $\left( {ON} \right)$is the radius of the rotating body
Now calculation of dimensional formula of force
Velocity: It is the distance covered per unit time so $v = \left( {\dfrac{d}{t}} \right)$
From here we can say that is the ratio of distance and times so the dimensional formula will be
 $\dfrac{L}{T}$ (Or) $\left[ {L{T^{ - 1}}} \right]$
Acceleration = it is the rate of change of velocity with time so,
We can say that $a = \dfrac{v}{t}$
Here velocity is divided by time again we will substitute the dimensional formulas of velocity band time to get the dimensional formula for acceleration
\[
  \therefore a = \left[ {\dfrac{{L{T^{ - 1}}}}{T}} \right] \\
   \to a = \left[ {L{T^{ - 2}}} \right] \\
 \]
Force: It is defined as the mass time of acceleration so,
$F = M \times A$
Now we will be using the dimensional formula of acceleration and mass to find out the dimensional formula of force
$\because F = M \times A$
The dimensional formula of force will also be the product of the dimensional formula of the other two quantities
So,
$
 \Rightarrow F = M \times L{T^{ - 2}} \\
   \Rightarrow F = \left[ {ML{T^{ - 2}}} \right] \\
 $
Now as $\left( {ON} \right)$is the radius of the disk so its dimension will be of a length so,
$r = \left[ {{M^0}{L^1}{T^0}} \right]$
AS Moment of Force = \[F \times r\]
$\therefore $ the dimensional formula for the moment of force will be
$
   \Rightarrow \left[ {ML{T^{ - 2}}} \right] \times \left[ {{M^0}{L^1}{T^0}} \right] \\
   \Rightarrow \left[ {{M^1}{L^2}{T^{ - 2}}} \right] \\
 $
The dimensional formula for the moment of force is $\left[ {{M^1}{L^2}{T^{ - 2}}} \right].$

Note: Dimensional formula of any quantity can be derived for the fundamental quantities if the relation between them is known. Dimensional Formulas are used to check whether a given formula is dimensionally correct or not. Dimensional Formulae become not defined in the case of the trigonometric, logarithmic, and exponential functions as they are not physical quantities.