Question

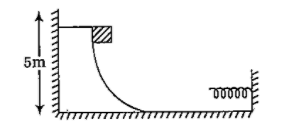
Consider the situation shown in the figure. A spring of spring constant \[400{\text{ }}Nm\]is attached at one end to a wedge fixed rigidly with the horizontal part. A \[40g\] mass is released from rest while situated at a height 5cm the curved track. The maximum deformation in the spring is nearly equal to (take \[g = 10m/{s^2}\]

(A) $9.8m$
(B) \[9.8cm\]
(C) $0.98m$
(D) $0.009km $

Answer 1

Hint In this situation energy from one form is converted into another form hence we can use the conservation of energy theorem with the given values to calculate the spring deformation
Formula Used:
\[{K_i} + {P_i} = {K_f} + {P_f}\]

Complete step by step answer
Since the block is released then initial velocity,$u = 0$and it will follow the curved path and compress the spring till the final velocity of block will be zero after that the spring will regain its position and the block will be thrown back.
Since it is a friction less path, no external force exists. Only conservative forces are present hence you can say that the mechanical energy is conserved between the point of drop till the point of maximum compression of spring.
\[{K_i} + {P_i} = {K_f} + {P_f}\] , where $K_i$ and $K_f$ are the initial and final kinetic energy ---(1)
And $P_i$ and $P_f$ are the initial and final potential energy
We know that potential energy at a height ‘h’ of mass ‘m’ is given by \[mgh\]where g is the acceleration due to gravity and the potential energy stored in the spring is $\dfrac{1}{2}k{x^2}$ where k is the spring constant and x is the displacement.
\[{K_i} = 0\]and\[{K_f} = 0\]as the initial and final velocities are zero
As you can see that the final potential of block is also zero since its final velocity is zero, but the elastic potential energy will be acting thus
Substituting these in equation (1),
\[0 + mgh = 0 + \dfrac{1}{2}k{x^2} \Rightarrow x = \sqrt {\dfrac{{2mgh}}{k}} = \sqrt {\dfrac{{2 \times 0.04 \times 10 \times 5}}{{400}}} = \dfrac{1}{{10}}m = 10cm \cong 9.8cm\]

Hence, the correct option is B.

Note
If a string is compressed or stretched then we see that work is done due to spring elasticity, this work done is stored in the spring in the form of elastic potential energy.