Question

Consider a body of 800 kg moving with a maximum speed $v$ on a road banked at\[\theta = {30^0}\] given \[\cos {30^0} = 0.87\]. Find the normal reaction on the body. Coefficient of friction \[{\mu _s} = 0.2\]. [Take radius, r=10m]
A. 10.4 kN
B. 12.6 kN
C. 11.6 kN
D. 8.3 kN

Answer 1

Hint:When the applied force increases, then the force of friction also increases. The maximum value of static friction is known as limiting friction.
If a body is moving with a maximum speed v on a road banked. Since the circular motion is such that v = vmax the tendency of the body is to move up the inclined plane.

Formula used:
Centripetal force is given as:
\[\dfrac{{m{v^2}}}{r}\]
Where m is the mass of the given body, r is the radius of the circle and v is the maximum speed.
Maximum friction,
\[{f_s} = {\mu _s}N\]
Where \[{\mu _s}\]is the coefficient of friction and N is the normal reaction between the two surfaces.

Complete step by step solution:
Given Coefficient of friction \[{\mu _s} = 0.2\].
Radius of circle, r=10m
\[\cos {30^0} = 0.87\]
Taking g=10m/\[{s^2}\]


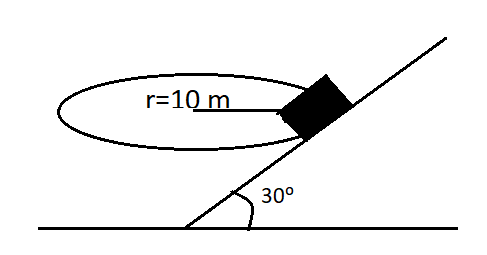
In a body force mg is in downward direction and normal reaction is along incline. Here the incline is in \[{30^0}\](in figure). The friction force is along incline and it is at maximum because it moves its maximum speed. Also a centrifugal force acts on it in an outward direction.

Now the normal reaction will be applied perpendicular to the inclined.

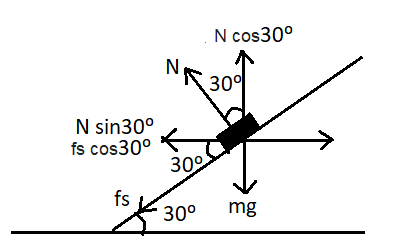
Image: Diagram showing resolving components.

After resolving along X axis and Y axis, we have
\[N\cos {30^0} = mg + {f_s}\sin {30^0}\]
As we know, maximum friction \[{f_s} = {\mu _s}N = 0.2N\]
Substituting all the values, we get
\[N\cos {30^0} = mg + {f_s}\sin {30^0}\]
\[\begin{array}{l} \Rightarrow N \cos {30^0} = mg + {f_s}\sin {30^0}\\0.87{\rm{ N = 800}} \times {\rm{10 + 0}}{\rm{.2N}} \times \dfrac{1}{2}\\ \Rightarrow N = \dfrac{{800}}{{0.77}}\\\Rightarrow N {\rm{ = }}10389.6{\rm{ N}}\\ \Rightarrow N {\rm{ = 10400 N}}\\ \therefore N {\rm{ }} \approx {\rm{ 10}}{\rm{.4 kN}}\end{array}\]
Therefore the normal reaction on the body is 10.4 kN.

Hence option A is the correct answer

Note: The banking of roads is the phenomenon in which the outer edges must curve roads above the inner edge to provide the centripetal force to the vehicles so that they can take safe turns.