Question

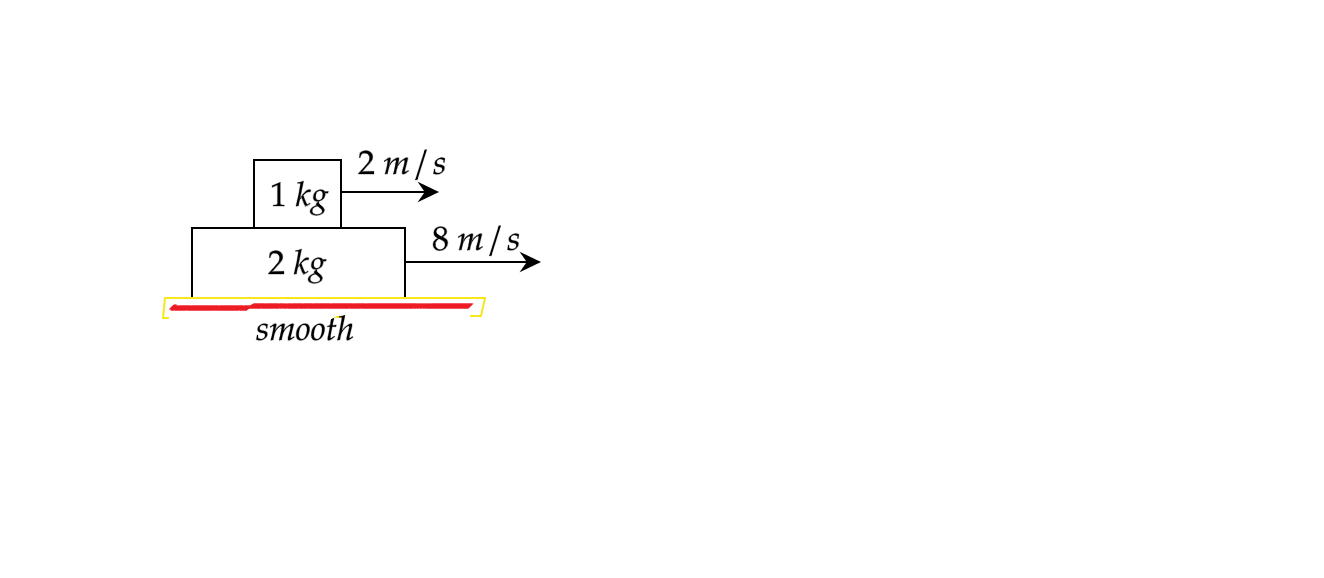
Coefficient of friction between two blocks shown in the figure is \[\mu =0.4\]. The blocks are given velocities of \[2m/s\] and \[8m/s\] in the direction shown in the figure. Find displacements of \[1kg\] and \[2kg\] blocks up to the instant when the relative motion between the blocks will stop.
 \[(g=10m/{{s}^{2}})\]

Answer 1

Hint: The relative velocity between the blocks will stop when both the blocks have the same velocity. So if we find the velocity at a certain instant after the start of motion between the blocks and equate them, we can get the time when the relative motion stops. To find the velocity at a certain instant, we need to find the accelerations of the two blocks and hence we must start with the forces acting on the block.

Formula Used:
 \[F=m.a\], \[v=u+at\], \[s=ut+\dfrac{1}{2}a{{t}^{2}}\], \[f=\mu N\]

Complete step by step solution:
The floor of the setup is smooth, so no frictional force acts on the \[2kg\] block because of the floor. A friction force will act on the \[1kg\] because the coefficient of friction between the two blocks has been given to us.

From Newton’s law of action and reaction, the reaction of the friction force acting on the \[1kg\] will act on the \[2kg\] block in the opposite direction.

When the relative motion between the two blocks stops, they move together as one single body. This is similar to the inelastic collision of bodies when they stick together after the collision.
So we can apply momentum conservation before and after the relative motion between the blocks stops, which states the sum of the momentum of the blocks before the relative motion stops will be equal to the momentum of the body after the relative motion stops.

Mathematically, we can express it as \[1kg\times (2m/s)+2kg\times (8m/s)=3kg\times v\] where \[v\] is the common velocity of the blocks after the relative motion stops.

Solving the above equation, we get \[v=\dfrac{18kg.m/s}{3kg}=6m/s\]

Friction force acting one the \[1kg\] block is equal to \[\mu N\] where \[N\] is the normal force acting on the block and \[N=mg\]

Hence the friction force will be \[\mu mg\] .

Substituting the values, we get \[f=0.4\times 1\times 10=4N\]

Now, the only force acting on the two blocks will be this friction force of \[4N\] (due to them being an action-reaction pair, as discussed in the hint section)

The friction force tends to oppose the motion of the body and hence, for the \[2kg\] block it acts against its direction of motion. But for the \[1kg\] block, it acts along its direction of motion (since the action must be opposite in direction to the reaction)

Acceleration of the \[1kg\] block is equal to the ratio of the force acting on it to its mass.

Hence, \[{{a}_{1}}=\dfrac{f}{{{m}_{1}}}=\dfrac{4}{1}=4m/{{s}^{2}}\] where \[{{a}_{1}}\] is the acceleration of the \[1kg\] block.

Similarly, acceleration of the \[2kg\] block \[({{a}_{2}})=\dfrac{-4N}{2kg}=-2m/{{s}^{2}}\]. The negative sign implies that the acceleration acts in a direction opposite to the direction of the motion of the block)
Now, we have to find the instant when the relative motion stops. To do that, we simply have to apply the first equation of motion to any of the blocks, that is \[v=u+at\] where \[u\] is the initial velocity, \[v\] is the final velocity, \[a\] is the acceleration of the block and \[t\] is the time taken.
Applying this equation to the \[2kg\] block, we get
\[\begin{align}
  & v=u+at \\
 & \Rightarrow 6=8+(-2)\times t\left[ \because {{v}_{final}}=6m/s \right] \\
 & \Rightarrow 2t=2 \\
 & \Rightarrow t=1s \\
\end{align}\]
Hence the relative motion stops in \[1s\] .
To find the displacement of the blocks, we need to apply the second equation of motion to both the blocks, that is \[s=ut+\dfrac{1}{2}a{{t}^{2}}\] where \[s\] is the displacement of the body and the meanings of the other symbols have been discussed above.
For the \[1kg\] block,
\[\begin{align}
  & {{s}_{1}}=(2m/s)\times 1s+\dfrac{1}{2}\times (4m/{{s}^{2}})\times {{(1s)}^{2}} \\
 & \Rightarrow {{s}_{1}}=2m+2m=4m \\
\end{align}\]
Similarly, for the \[2kg\] block,
\[\begin{align}
  & {{s}_{2}}=(8m/s)\times 1s+\dfrac{1}{2}\times (-2m/{{s}^{2}})\times {{(1s)}^{2}} \\
 & \Rightarrow {{s}_{2}}=8m-1m=7m \\
\end{align}\]

Hence the displacements of the \[1kg\] and the \[2kg\] blocks are \[4m\] and \[7m\] respectively.

Note: Students often make the mistake of applying the friction at every interface because the value of the coefficient of friction is given. It must be noted that friction does not act on smooth surfaces, hence there is no friction acting between the floor and the \[2kg\] block. If you apply friction at this interface, you’ll never get the correct answer.