Question

Circles of radii $3$ and $4$ intersect orthogonally. The area common to the two circles is
A. $8\pi + 12 - 7{\tan ^{ - 1}}\dfrac{4}{3}$
B. $8\pi - 12 - 7{\tan ^{ - 1}}\dfrac{4}{3}$
C. $8\pi - 12 + 7{\tan ^{ - 1}}\dfrac{3}{4}$
D. $\dfrac{{9\pi }}{2} - 12 + 7{\tan ^{ - 1}}\dfrac{3}{4}$

Answer 1

Hint: In this question, we are given the radii of circles and we have to find the common area of both the circles. First step is to draw the figure. Then, find the area of quadrilateral AOBO’ which is made by the intersection of circles. Now, shade that part of the quadrilateral which is not common in both circles and find the particular area by subtracting the connecting sector from the area of the quadrilateral. Same for the other portion. Lastly, subtract the shaded area from the total area. Required area will be the area of the common part.

Complete step by step solution: 
Given that,

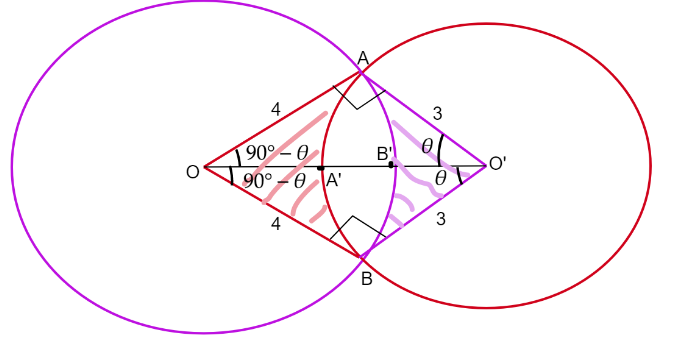
Radii of the circle are $3$ and $4$ units which intersect orthogonally.
Area of the quadrilateral AOBO’$ = $ $2 \times $ area of triangle OAO’
Therefore, $Ar.AOBO' = 2 \times \left( {\dfrac{1}{2} \times 4 \times 3} \right) = 12$
Now, the area of the portion $AOBA'$(Red shaded part) $ = Ar.AOBO' - ArAO'BA'$
$ = 12 - \left( {\dfrac{1}{2}{{\left( 3 \right)}^2}\left( {2\theta } \right)} \right)$
$ = 12 - 9\theta $
Similarly, the area of the portion $AO'BB'$(Purple shaded part) $ = Ar.AOBO' - ArAOBB'$
$ = 12 - \left( {\dfrac{1}{2}{{\left( 4 \right)}^2}\left( {2\left( {{{90}^ \circ } - \theta } \right)} \right)} \right)$
Write the angle in radian terms,
$ = 12 - 16\left( {\dfrac{\pi }{2} - \theta } \right)$
$ = 12 - 8\pi + 16\theta $
Therefore, Area common to the two circles ($AA'BB'$)$ = Ar.AOBO' - Ar.AOBA' - Ar.AO'BB'$
$ = 12 - \left( {12 - 9\theta } \right) - \left( {12 - 8\pi + 16\theta } \right)$
$ = 8\pi - 12 - 7\theta - - - - - \left( 1 \right)$
Here in right- angled triangle $AOO'$,
$\tan \theta = \dfrac{{perpendicular}}{{base}}$
$\tan \theta = \dfrac{4}{3}$
$\theta = {\tan ^{ - 1}}\dfrac{4}{3}$
Putting the above value in equation (1),
$Ar.AA'BB' = 8\pi - 12 - 7{\tan ^{ - 1}}\dfrac{4}{3}$
Hence, Option (B) is the correct answer i.e., $8\pi - 12 - 7{\tan ^{ - 1}}\dfrac{4}{3}$.

Note: The key concept involved in solving this problem is the good knowledge of formulas of areas. Students must remember that to solve such question making figures is mandatory. Without figure questions it will be confusing. Also, while taking the angle of the sector, double the angle and both the triangles have different angles.