Lattice Energy: General Discussion, Calculation and Examples for JEE

In an ionic compound, the strength of the ionic bond between two oppositely charged ions depends mainly on the charge of ions and the distance between the ions when they are in a crystal form. An approximate estimate of the strength of ionic bonds can be obtained by calculating lattice energy. Lattice energy is the energy change accompanied when oppositely charged ions in the gas phase come together and form crystalline ionic solids. As it is difficult to isolate gaseous ions, the experimental determination of lattice energy is difficult. However, it can be estimated by using the Born-Haber cycle. 

Lattice Energy and Lattice Enthalpy

As mentioned, lattice energy is defined as the heat of formation accompanied when 1 mole of crystalline ionic solid is formed from its constituent ions which are in their gaseous state. For example, the lattice energy of NaCl is the energy change of reaction when sodium and chlorine ions react to form NaCl crystal and is equal to -786 $\dfrac{kJ}{mol}$. 

$Na^+~(g)+Cl^-~(g)\rightarrow NaCl~(s)$

We can define lattice enthalpy as

• The lattice dissociation enthalpy is the enthalpy change required to convert one mole of crystalline ionic solid into its constituent gaseous ions. It is always positive. i.e, endothermic.

• The lattice formation enthalpy is the enthalpy change accompanying the formation of  1 mole of solid ionic crystal from respective gaseous ions. They are always negative. i.e, exothermic.

The lattice energy of an ionic solid is given by modified Coulomb's Law

$U=-\dfrac{k^{\prime} Q_{1} Q_{2}}{r_{0}}$

Where

U = The amount of energy required to dissociate 1 mol of an ionic solid into the gaseous ions. It is a positive number

 k’ = the proportionality constant.

Q₁ and Q₂= The charges on the ions

r₀ = The internuclear distance. 

The following equation gives the relation between lattice energy and lattice enthalpy at constant pressure P. The lattice enthalpy formula is given by

$\Delta U_{lattice}=\Delta H_{lattice}-P \Delta V_{m}$

Where,

$\Delta U_{lattice}=$ Lattice energy change or molar internal energy change

$\Delta H_{lattice}=$ Lattice enthalpy 

$\Delta V_{m}=$ Change in molar volume due to formation of the lattice.

Energy is the state of a system and it is energy associated with the molecular configuration and motion of molecules constituting the system. Enthalpy can be referred to as the total heat content of a system. Enthalpy change is an energy change between two states of a particular system or heat added or removed when a chemical change happens. 

How to Calculate Lattice Energy?

The lattice energy value of an ionic solid affects physical properties like solubility, hardness, volatility, etc. There are two methods by which the lattice energy can be calculated.

1. Theoretical estimates of lattice energy by empirical equations (Born-Lande equation)

2. Using the Born-Haber cycle method; in this method, experimental values of enthalpy changes are used to calculate the lattice enthalpies.

1. Born-Lande equation

Lattice energy can be calculated from the Born-Lande equation which is derived from the electric potential of the ionic lattice and repulsive potential energy. It is given by

$\Delta U_{lattice}=-\dfrac{N_{A} M z^{+} z^{-} e^{2}}{4 \pi \varepsilon_{0} r_{0}}\left(1-\dfrac{1}{n}\right)$

Where

N_A = Avogadro constant

M = Madelung constant, related to geometry of crystal

Z⁺ = Charge number of the cation

Z- = Charge number of the anion 

e = elementary charge, 1.6022$\times$ 10^-19 C

$\varepsilon_{0}=$ Permittivity of free space 8.854$\times$ 10^-12 C²J^-1m^-1

r₀ =nearest-neighbour distance between ions

n = Born constant (between 5 and 12)

2.  Born-Haber Cycle Method

The Born-Haber cycle method is mainly used to calculate the lattice energies of fully ionic solids such as certain alkali halides. This method applies Hess’s law on following enthalpies to calculate the lattice energy. They are

1. The standard enthalpy of formation of ionic compounds from the gaseous state of ions

2. The standard atomisation enthalpy is the enthalpy change occurring when a compound's bonds are broken and the component atoms are separated into single atoms at standard state (298.15 K and 1 bar)

The standard atomisation enthalpy is the enthalpy change accompanied when 1 mole of gaseous atoms is formed from the element in its standard state and is always positive. This is because we need to supply energy to divide an element into its separate gaseous atoms. An understanding of the following concepts is required to calculate the lattice energy

• Ionisation energy:  It is the amount of energy required to remove an electron from an isolated gaseous atom/ion.

• Electron affinity: It is the amount of energy released when an electron is added to a gaseous atom to form a negatively charged ion.

• Dissociation energy: Energy required to break the bond in a molecule.

• Sublimation energy: Energy required to change from solid phase to gas phase directly.

The following are the steps in the Born-Haber cycle 

1. Find the energy of ionic solid which is the heat of formation of ionic solid. Consider the  Born-Haber cycle for NaCl given in the below diagram. Here the heat of formation of NaCl is -411 kJmol^-1.

2. Find the changes in enthalpy to turn the elements into their gaseous state. The atomisation enthalpy of sodium to convert it to a gaseous state is +107 kJmol^-1.

3. Generally, nonmetals will exist as polyatomic species. The energy required to change Cl₂ into 2Cl atoms must be added to the value obtained in Step 2 which is +122 kJmol^-1.

4. To get ionic forms of constituent atoms, we need to ionise them. The ionisation energy of the metal will be added (for sodium it is +496 kJ mol^-1)  and that of non-metal will be subtracted to the value from Step 3 (for chlorine it is -349 kJ mol^-1). As there will be the release of energy associated with the addition of an electron, the energy is subtracted. During ionisation of sodium as energy is absorbed, the ionisation energy is added. 

5. Last step the metal and nonmetal will be combined to form the ionic solid and release lattice energy. The Lattice energy can be given as the difference between the value from Step 1 and the value from Step 4.

Hence 

Lattice formation enthalpy for NaCl = -411-(107+122+496-349) kJ mol^-1

  = -787 kJ mol^-1

This is the standard lattice enthalpy of NaCl.

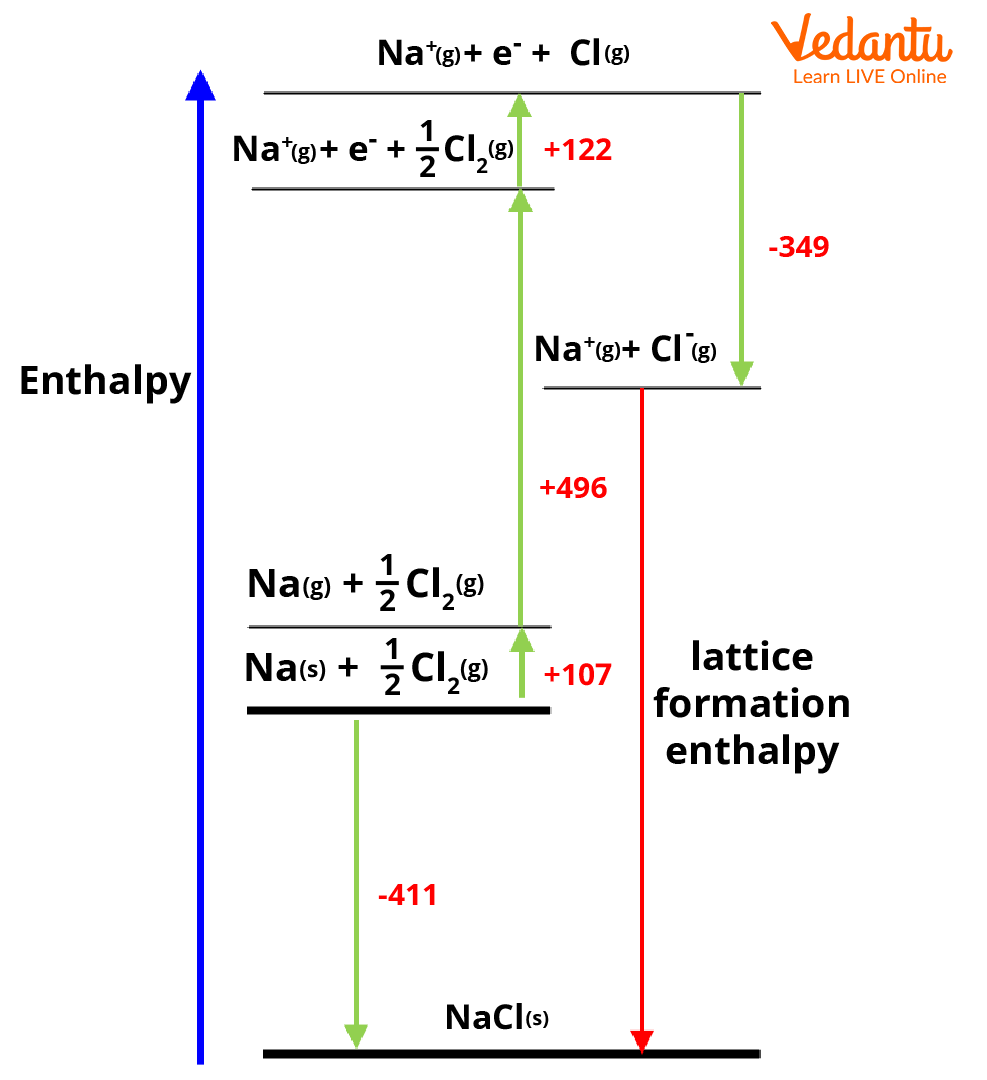
Born-Haber cycle for NaCl

Factors Affecting Lattice Energy

The factors affecting lattice energy are as follows:

• The charges on the ions

• Radius of Ions  (It affects the distance between the ions)

The Charges on the Ions

The ionic bond is formed due to the electrostatic force of attraction between the opposite ions. Hence, the bond should be stronger as the charge on the ions becomes larger. This means lattice energies will be more if the charge on the ion becomes larger. Consider the lattice energy example of barium oxide (BaO) and NaCl, both have similar crystal structures and therefore have the same Madelung constant. The lattice enthalpy of BaO is  −3054 $\dfrac{kJ}{mol}$ which is very much higher than that of sodium chloride (lattice enthalpy of NaCl = −786 $\dfrac{kJ}{mol}$). This is because BaO has charge numbers of (+2,−2) which are higher than NaCl charge numbers (+1,−1). According to the Born–Lande equation, the difference in charge numbers is the principal reason for the large difference in lattice energies.

The Radius of the Ions

When the ions are small, the bond between them is strong. This is because smaller ions will be closer in a lattice and thus the electrostatic attractions will be more in this case. So when the ions are closer, they will have higher lattice energy. In a periodic table, as we move down a group atomic radii increase, hence lattice energy decreases down the group. For example, considering alkali metal halides, the higher lattice energy will be for LiF and the lowest lattice energy will be for CsI. So as the atomic size of ions increases the lattice energy decreases due to the less electrostatic force between the ions. 

Conclusion

Ionic solids are very stable compounds. The lattice energy of the solid structure gives an approximate strength of the ionic bond. The lattice energy is the energy change that occurs during the formation of an ionic compound from gaseous ions which is an exothermic process. It can also be defined as the energy which is needed to break the ionic compound into gaseous ions and it is an endothermic process. However, lattice energy measurement is difficult. 

The lattice energy can be measured by a theoretical estimate by the Born-Lande equation or by the Born-Haber cycle which uses experimental enthalpy values. The main factors affecting lattice energy are the charge of the constituent ions and the size of ionic radii.