




What is Rate of Radioactive Decay and Half-Life?
At times, elements undergo radioactive decay naturally. During this process, all the atoms don’t transform into the atoms of a different element instantaneously. The process of atom decay will take place over a prolonged period of time and the half-life is an important measurement value used to express this rate of decay.
Half-Life and the Factors Affecting It
Hence, the half-life is the time taken by half of the atoms present in an element at the beginning to decay or change into atoms of another element. In other words, during a particular half-life, half of the original nuclei of the substance will decay or disintegrate.
Take a look at the image below.
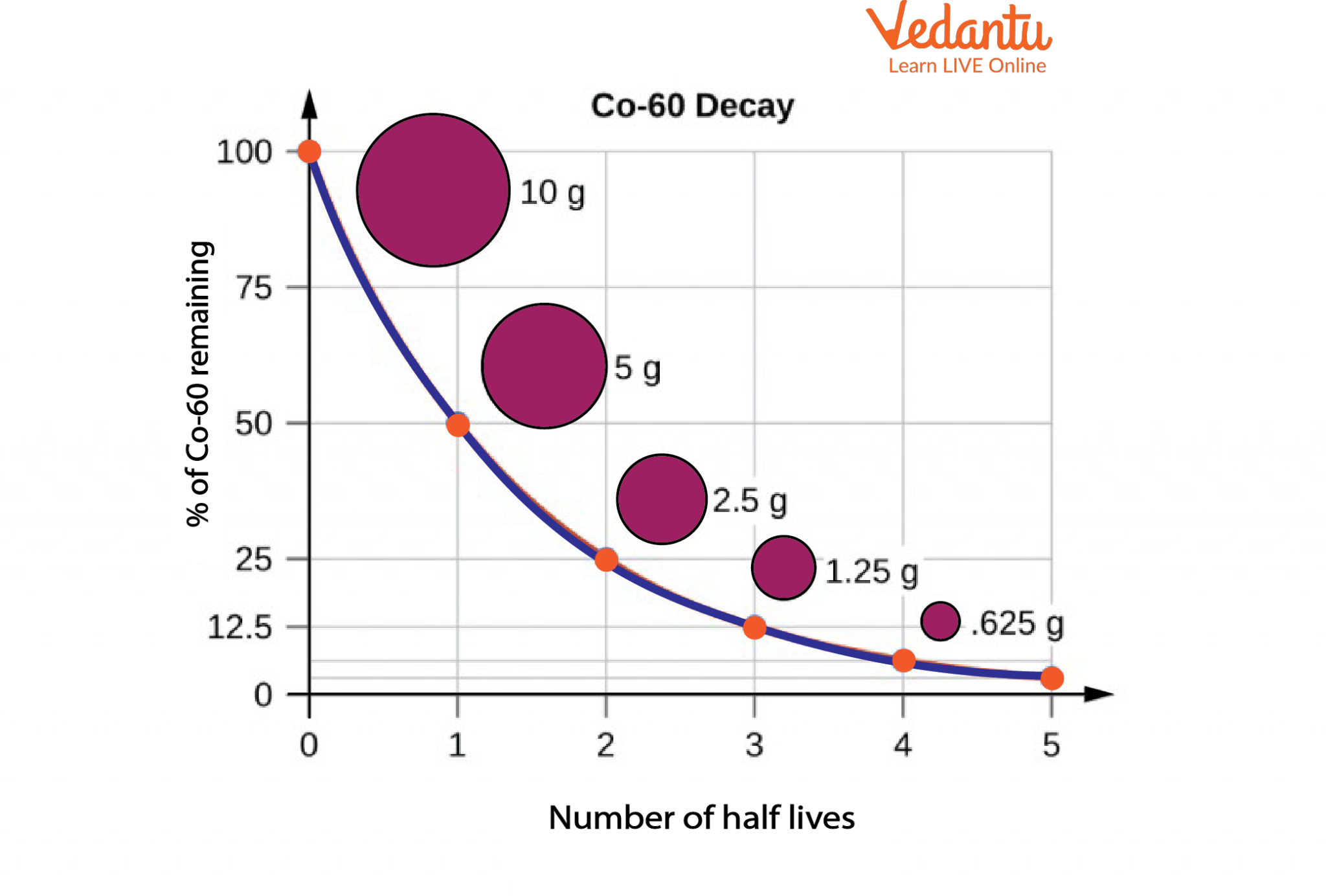
Radioactive Decay and Half-Life of Co-60
The graph in the image above illustrates the percentage of radioactive Co-60 remaining after each half-life. It can be seen that after the first half-life, only 50% of Co-60 is remaining, i.e., out of the initial 10g only 5 g is left behind. Half-lives can be very long and the material undergoes continuous disintegration and decay over its lifecycle.
Factors Affecting Half-life and Radioactive Decay
Each radioactive isotope will have a unique half-life that is dependent on factors such as temperature, concentration etc. These factors will change the nuclide mass and the time it takes to attain this change. The half-lives of radioactive isotopes have been found to range from a fraction of a second to 10 billion years.
Order of a Reaction
Order of a reaction gives the relationship between the rate of reaction and the molar concentration of the species reacting, i.e., it is the exponent to which the concentration of any reactant in the law of rate of a reaction is raised.
For example, consider the reaction $xX+yY\to {{Z}_{1}}+{{Z}_{2}}$
The order of the reaction with respect to the reactants X and Y is x and y respectively. The overall order of the reaction is x+y.
The Half-Life of a First-Order Reaction
The rate of reaction of a first-order reaction is directly proportional to the concentration of only one of the reactants participating in the reaction. For example, if the concentration of any reactant is reduced by half, the rate of the reaction also reduces by half. Similar to any decomposition reaction, a first-order reaction can have up to two reactants.
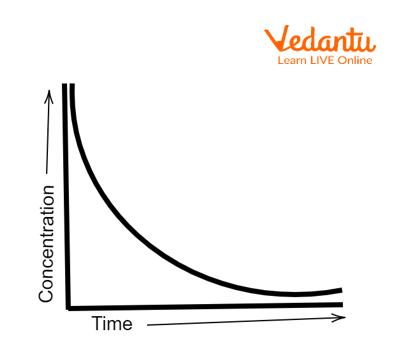
Concentration vs Time graph
A few examples of first-order reaction include the hydrolysis of aspirin, decomposition of hydrogen peroxide into water and oxygen etc.
The half-life of a first-order reaction is constant and independent of the concentration of the reactants.
Derivation of the Half-life Formula
The rate constant for a first-order reaction is expressed as:
$k = \frac{2.303}{t}log\frac{\left [ R \right ]_{o}}{\left [ R \right ]}$
In the above expression, k is the rate constant, t1/2 is the time, ${\left [ R \right ]}$o is the initial concentration of the reactant, and ${\left [ R \right ]}$ is the current concentration of the reactant.
Since at half-life, the concentration of the reactant reduces to half, t = t1/2 (Half-life) and $\left[ R \right]=\frac{{{\left[ R \right]}_{0}}}{2}$ i.e., the concentration reduces to half of the initial concentration.
$k = \frac{2.303}{t_{1/2}}log\frac{\left [ R_{o} \right ]}{\left [ R_{o} \right ]/2}$
By rearranging the above equation, the half-life of a first-order reaction can be obtained to be
\[ {{t}_{1/2}}=\frac{2.303}{k}log\left( 2 \right)\]
\[ {{t}_{1/2}}=\frac{0.693}{k}\]
The Half-Life of a Second-Order Reaction
The sum of the exponents in the rate of law equation is equal to two in a second-order reaction. In other words, the rate of decay in such reactions is dependent either on the concentration of a second-order reactant or the concentration of two first-order reactants.
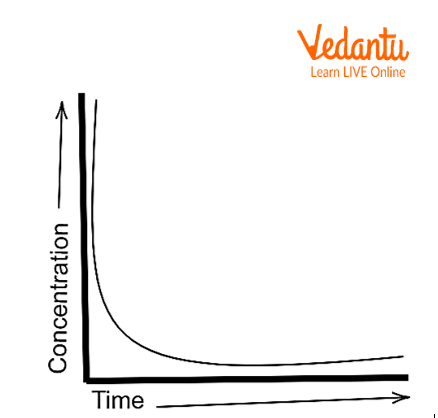
Concentration vs Time
The general expression of the rate of second-order reactions is given by
$r = k\left [ A \right ]^{x}\left [ B \right ]^{y}$
where x+y is the order of the reaction, A and B are reactants, and k is the rate constant.
A few examples of second-order reactions are as follows:
\[{{H}^{+}}+O{{H}^{-}}\to {{H}_{2}}O\]
\[2N{{O}_{2}}\to 2NO+{{O}_{2}}\]
Derivation of the Half-Life Formula
The rate constant of a second-order equation expressed in integrated form is
$\frac{1}{\left [ R \right ]_{t}}-\frac{1}{\left [ R \right ]_{o}} = kt$
Since at half-life, the concentration of the reactant reduces to half, t = t1/2 (Half-life) and [R] = [R]o/2, the above equation becomes
$\frac{1}{\frac{\left [ R \right ]_{0}}{2}}-\frac{1}{\left [ R \right ]_{o}} = kt_{1/2}$
By rearranging the terms of the above equation, the half-life of a second-order reaction can be obtained.
$t_{1/2} = \frac{1}{k\left [ R \right ]_{o}}$
The Half-Life of a Third-Order Reaction
A third-order reaction is dependent on both the time and concentration of the reactant. It is an experimental value determined from the reaction step that is the slowest.
A few examples of third-order reaction are as follows:
$2NO+C{{l}_{2}}\to 2NOCl $
$2NO+{{O}_{2}}\to 2N{{O}_{2}}$
The rate of reaction of a third-order reaction can be expressed as:
$\frac{1}{2\left [ R \right ]^{2}}-\frac{1}{2\left [ R \right ]^{2}_{o}} = kt$
Since at half-life, the concentration of the reactant reduces to half, t = t1/2 (Half-life) and [R] = [R]o/2, the above equation becomes
$\frac{4}{2\left[ R \right]_{o}^{2}}-\frac{1}{2\left[ R \right]_{o}^{2}}=k{{t}_{1/2}} $
$\frac{3}{2\left[ R \right]_{o}^{2}}=k{{t}_{1/2}}$
${{t}_{1/2}}=\frac{3}{2k\left[ R \right]_{o}^{2}}$
Summary
Radioactive decay happens in most substances and half-life is the measure that expresses the time it takes for elements in a substance to reduce to half their initial concentration. The half-life of radioactive isotopes is unique and dependent on various factors including temperature and concentration of the reactants. Half-life can be measured for first, second, and third-order reactions by substituting t = t1/2 (Half-life) and $\left[ R \right]=\frac{{{\left[ R \right]}_{0}}}{2}$ in the rate constant equation of respective reactions. One of the most important applications of half-life is carbon dating which determines the age of useful artifacts by studying their half-life period.
FAQs on Half-Life of First, Second and Third Order Reactions for JEE
1. State a practical application of half-life determination in radiation study.
Half-life determination is important to control radiation because it gives an idea about the amount of long-lived and short-lived radionuclides, say in a decommissioning of sites that were once actively used in radioactive processes and activities. In such cases, short-lived substances can be significantly reduced through radioactive decay whereas it takes very long to disintegrate the long-lived radionuclides. Hence, it requires other procedures like demolition of buildings, removal of contaminated soil, or removal of contaminated materials in the building.
2. Briefly explain the relationship between radioactive decay and the order of the reaction.
The half-life of a first-order reaction is completely independent of the order of the reaction and hence is a constant under certain established conditions unlike zeroth-order reactions and second-order reactions. However, when two reactions of the same order are subjected to a radioactive decay process, the one with the faster reaction will comparatively have a shorter half-life and vice versa. It is easier to determine the time required to complete a percentage of the decay in a first-order reaction if the rate constant is known.


































