Effective Nuclear Charge for JEE

Coulomb’s law is used to predict the attractive or repulsive force between two charged bodies and it is directly proportional to the product of charges and inversely proportional to the square of the distance between them. This law can be used to predict the energy of electrons in hydrogen which has one proton in the nucleus and one electron and in hydrogen like atoms, e.g.,  Helium ion. However, this law cannot be used to predict the energies of electrons in multi-electron atoms and ions.

In a multi-electron atom, the electron in question has to interact with the nucleus and with all other electrons. Thus, each electron in such systems experiences two types of force: (1) attraction to the nucleus and (2) repulsion from other electrons. The presence of multiple electrons results in more repulsive force and this decreases the nuclear attraction to some extent. Thus, the amount of nuclear charge or positive charge experienced by an electron when it is present in a multielectron atom or ion is called effective nuclear charge.

What is Effective Nuclear Charge?

The energy of an electron in a multi-electron atom depends on both its principal quantum number(shell) and on its azimuthal quantum number(subshell). In a given principal quantum number, the energy of orbitals increases in the order s<p<d<f. But for higher energy levels, there are differences in the energy of orbitals and it will not follow the above order.

For example,  4s < 3d and 6s < 5d ; 4f < 6p.

The different energies of the subshells are due to the mutual repulsion experienced by the electrons. 

In a multi-electron atom when the total attractive interactions are more than repulsive interactions, it will be stable. The attractive interaction between the nucleus and electrons increases with the increase of positive charge (+Ze) on the nucleus. This attractive interaction for the outer shell electron will be lower because of a phenomenon called Shielding. The cause of this is the partial screening of the positive charge of the nucleus by the inner shell electron. Due to the shielding of inner-shell electrons, the outer electrons will not have the full experience of the positive charge of the nucleus.

The effective nuclear charge definition is as follows: It is the net positive charge experienced by the outer electrons due to shielding of positive charge by inner shell electrons. The effective nuclear charge is denoted by Zeff .

Calculation of Effective Nuclear Charge 

To calculate, we'll write out an atom's orbitals and divide them into ‘groups’. Each change in shell number creates a new group; the s and p subshells belong to the same group, while the d and f orbitals belong to their own. You write out all of the orbitals in parentheses until you reach the group of the electron-of-interest, as seen below:

(1s), (2s, 2p), (3s, 3p), (3d), (4s, 4p), (4d), (4f), (5s, 5p), and so on.

• Electrons in the Same Group: Every additional electron in the same group as the chosen electron contributes 0.35 to $\sigma$ (do not count the chosen electron).

• If the electron-of-interest is in a d or f subshell, every electron in groups () to the left contributes 1.00 to $\sigma$. This indicates that all electrons in the same shell with a smaller value of l, as well as all electrons in lower shells, shield d and f electrons completely ( n ), due to the poor shielding effect of d electrons.

• All electrons in the next lower shell (n - 1) contribute 0.85 if the electron-of-interest is in an s or p subshell. Furthermore, all electrons in lower shells contribute 1.00 to $\sigma$. This means that s and p electrons are shielded 85% by electrons one shell lower and 100% by all electrons in shells n - 2 and lower.

• 1s electrons $\sigma=0.3$ of 1s electron for every element.

Slater’s Rules

First, write all the orbitals in the atom until the electron of interest. The orbitals are separated by groups. The new shell number is another group. Also in the same shell number, s and p subshells are in the same group but d and f form their own group. The orbitals must be written based on the increasing energy. The groups are (1s)(2s,2p)(3s,3p)(3d)(4s,4p)(4d)(4f)(5s,5p) etc.

Rules for electrons in the same group as electron-of-interest: Without considering the electron-of-interest, each electron in the same group contributes 0.35 to the shielding constant (S). This means 35% shielding by electrons in the same group with each other.

Rules for electrons to the left of  the group containing  electron of interest: 

• If the electron-of-interest is in a d or f subshell, then all electrons in groups to the left of the group having electron-of-interest contribute 1.00 to the shielding constant. This means 100% shielding of d or f subshell electrons by inner shell electrons.

• When the electron-of-interest is in an s or p subshell, the electrons in (n-1) contribute 0.85 to s and the lower shell electrons 1.00 to s. 

1s electrons in an atom always have a shielding constant of 0.3.

Consider a Neon atom, it has nuclear charge 10 (Z=10) and electronic configuration 1s22s22p6.

The group will be (1s2) (2s22p6).

If the electron-of-interest is 2p electron. Based on the rules,

then S = 2 ×  0.85 + 7 × 0.35 = 4.15

Zeff  = Z - S = 10 - 4.15 = 4.85

Now, let us calculate Zeff for a 3d-electron in a zinc (Zn, Z= 30) atom.

The groups are (1s2) (2s22p6)(3s23p6)(3d10)

S = 0.35×9+1×18 = 21.15

Zeff  = Z - S = 30 - 21.15 = 8.85

Values of Effective Nuclear Charge

The effective nuclear charge table shows the value of effective nuclear charge for different elements.

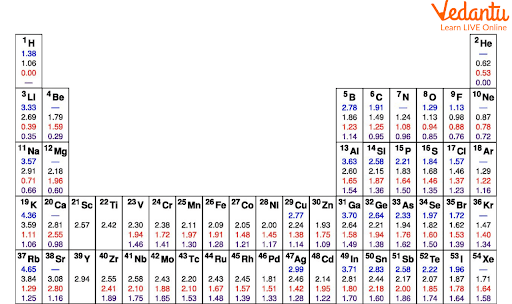
Values for Effective Nuclear Charge Table

Effective Nuclear Charge Trends

Zeff in a specific shell or subshell- The Zeff for electrons in a given shell and subshell increases as the atomic number increases; this tendency is observed both across and down the periodic table.

Understanding trends in valence Zeff is important for valence electrons since the valence Zeff determines atomic/ionic characteristics and chemical reactivity. As the valence shell and/or subshell change as the atomic number increases, the trends in the valence Zeff are not simple.

Down the Group:- As we go down the group of the periodic table, the valence  Zeff increases as the atomic number increases down the group.

Along a period:

Periods 1-3 (s and p only): As we go across periods 1-3, the shell remains constant as Z increases and the subshell changes from s to p. In these periods, there is a gradual increase in valence Zeff. For example, the effective nuclear charge of magnesium is 3.31 at the periphery while the effective nuclear charge of chlorine is 6.12 at the periphery. This indicates that Zeff increases along a period.

In periods 4 and 5 in the d subshell, effective nuclear charge shows an exceptional change in 4d subshell.

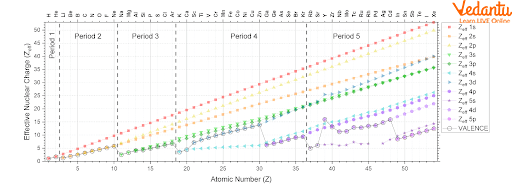
Trend of the Effective Nuclear Charge with Atomic Number

Conclusion

A nuclear charge is equal to the electric charge of a nucleus of an atom. The effective nuclear charge is the net attractive positive charge of nuclear protons acting on the electrons in a multi-electron atom or ion. This will be always less than the actual nuclear charge due to the shielding effect. The shielding effect means the decrease of the attractive electrostatic interactions between nuclear protons and valence electrons due to the partially or fully filled inner shells. This effect increases as the number of inner shells of electrons increases. The calculation of effective nuclear charge requires the value of shielding constant which can be determined by Slater’s rules.