How to Apply Malus Law: Solved Examples and Common Mistakes
Malus Law is a fundamental concept in light and optics, directly relevant for JEE Main. It describes how the intensity of a beam of plane-polarized light changes as it passes through a polarizing filter, depending on the angle between the light’s initial polarization direction and the filter’s transmission axis. Mastery of this law enables accurate solutions of problems on polarization, a recurring topic in competitive exams.
Malus Law helps JEE aspirants understand how light intensity varies with angle in experiments involving polarizers. This law not only appears in conceptual MCQs but is also essential in solving numericals where cos²θ dependence is tested. SEMANTIC_VARIANTS like “Malus law formula,” “Malus law example,” and “Malus law graph” anchor learning to both theoretical understanding and mathematical application.
What is Malus Law?
Malus Law states: When completely plane-polarized light passes through a polarizer, the transmitted intensity is given by the initial intensity multiplied by the cosine squared of the angle between light's polarization direction and the polarizer's axis. This means as the angle between the polarization and the filter increases, the transmitted light becomes weaker, reaching zero if the axes are perpendicular.
Malus Law Formula & Explanation
The central Malus law formula is:
| Formula | Variables |
|---|---|
| I = I₀ cos²θ | I: Transmitted intensity I₀: Initial intensity θ: Angle between light's polarization and polarizer’s axis |
Here, I₀ is the intensity entering the analyzer, θ is measured from the polarization direction to the transmission axis of the polarizer. If θ is zero, all light passes through; if θ = 90°, transmitted intensity drops to zero.
Derivation of Malus Law
The derivation connects light’s electric field vector to intensity. Let the incident electric field be E₀ and the angle between E₀ and the analyzer axis be θ.
- The electric field component parallel to the analyzer is E = E₀ cosθ.
- Since intensity is proportional to the square of the electric field, I ∝ E².
- Thus, I = I₀ cos²θ, where I₀ ∝ E₀².
This stepwise reasoning allows direct application in JEE Main numericals. Remember, Malus Law only applies to already polarized light entering the analyzer.
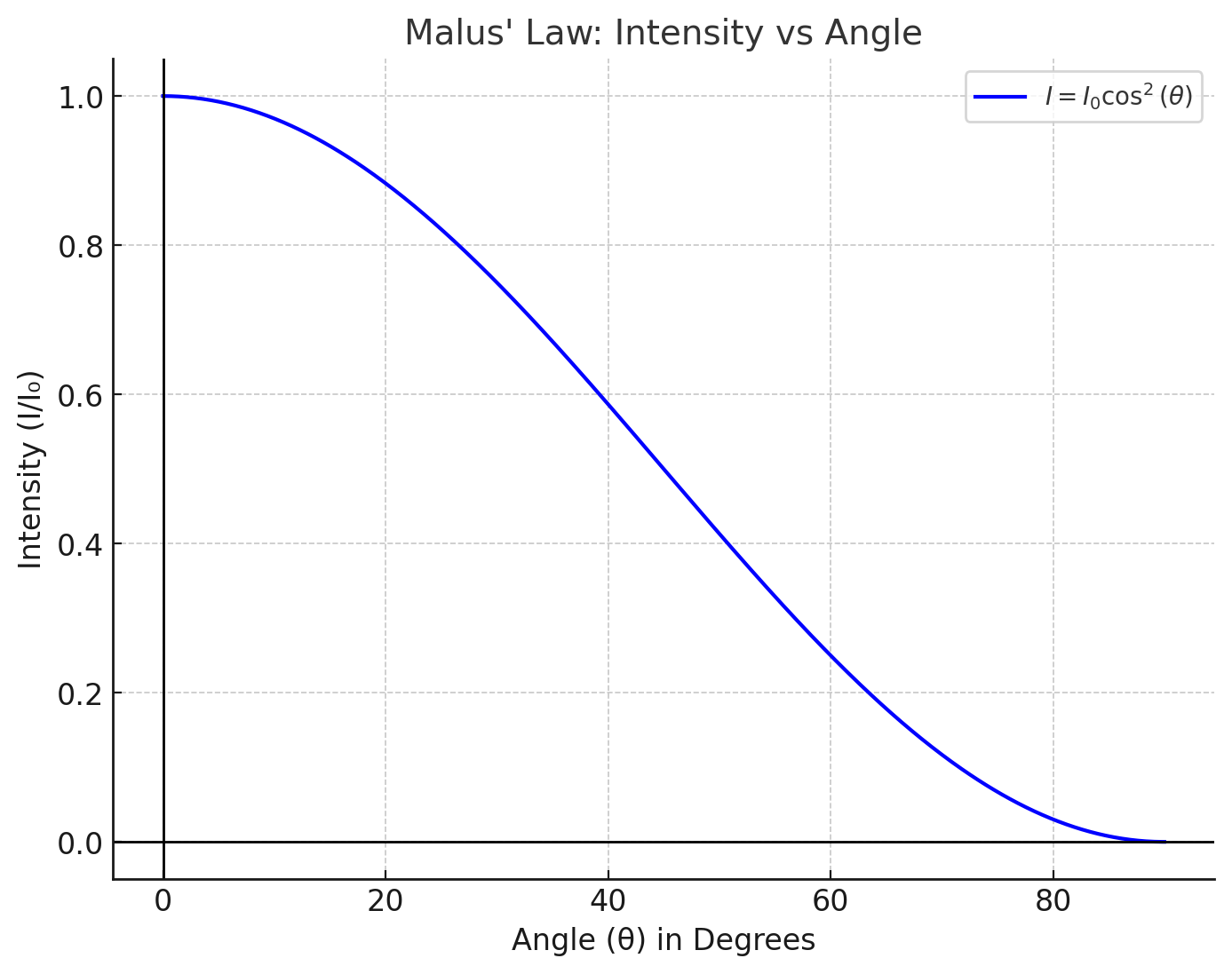
Malus Law Graph: Intensity vs Angle
Malus law graphically shows how transmitted intensity varies as the polarizer is rotated with respect to the incoming polarization. The common graph is I vs θ, a smooth cos²θ curve peaking at θ = 0°, falling to zero at 90°.
Notice at θ = 45°, intensity reduces to half, and a full extinction occurs at θ = 90°. Adjusting the polarizers demonstrates this experimentally, reinforcing how Malus law quantifies polarization effects.
Worked Example: Malus Law in JEE Numericals
Q: Plane-polarized light of intensity 8.0 W/m² passes through a polarizer with θ = 60°. What is the emerging intensity?
- Given: I₀ = 8.0 W/m², θ = 60°
- Apply Malus Law: I = I₀ cos²θ
- cos 60° = 0.5 ⇒ cos²60° = 0.25
- I = 8.0 × 0.25 = 2.0 W/m²
Thus, the intensity after the analyzer is 2.0 W/m².
Practical Applications of Malus Law
JEE frequently tests the real-world use of Malus Law. Below are typical cases:
- Analyzing sunglasses and anti-glare filters using polarization
- Measuring the state of polarization in optical labs
- Determining unknown polarization directions
- Studying stress patterns in transparent materials
In the lab, the classic experiment involves two polarizing sheets and measuring light intensity as one is rotated—demonstrating the cos²θ dependence directly.
Malus Law vs Brewster Law: Key Differences
| Malus Law | Brewster Law |
|---|---|
| Relates transmitted intensity to angle of analyzer | Gives the angle for maximum polarization at a surface |
| I = I₀ cos²θ, for plane-polarized incident light | n = tan θB, determines Brewster angle |
| Applies to any number of polarizers | Relevant for unpolarized light reflection/refraction |
For more on this, see the in-depth guide on Brewster’s Law.
Malus Law for Multiple Polarizers
When three polarizers are used, the intensity after each stage is calculated stepwise:
- First polarizer: converts unpolarized to polarized, halves the intensity
- Second and third: apply Malus Law with respective angles
- Net intensity: I = (I₀/2) × cos²θ₁ × cos²θ₂ (θ₁, θ₂: relative angles)
A counter-intuitive result is that with two crossed polarizers (θ = 90°), no light emerges, but inserting a third at 45° between them allows some light through.
Tips, Pitfalls, and Key Points on Malus Law
- θ is always the angle between the light’s polarization direction and analyzer axis
- Malus Law does not apply directly to unpolarized light; only to polarized beams entering the analyzer
- Always use cos²θ, not just cos θ
- For θ = 0°, all intensity passes; for θ = 90°, transmission is zero
- Read questions carefully for reference angle and intensity definitions
To dive deeper into the properties of polarized light, the dedicated Polarization of Light resource on Vedantu offers detailed illustrations and problem sets.
In summary, Malus Law is a central JEE Mains concept for wave optics, giving a precise mathematical link between the angle of a polarizer and the intensity of emerging light. Practicing its applications ensures accuracy in both conceptual and numerical sections. Review related principles on electromagnetic waves and optics for full topic mastery.
FAQs on Malus Law Explained: Statement, Formula & Stepwise Derivation
1. What is Malus law in Physics?
Malus law states that when completely polarized light passes through a polarizer, the transmitted intensity is proportional to the square of the cosine of the angle between the light’s polarization direction and the axis of the polarizer.
Key points:
- Malus law formula: I = I0 cos2θ
- I = transmitted intensity
- I0 = initial intensity
- θ = angle between polarization and polarizer axis
2. What is the equation for Malus's law?
The Malus law equation is written as:
I = I0 cos2θ
- I0: Initial intensity of the polarized light
- θ: Angle between the light’s polarization and the polarizer axis
- This formula helps calculate the transmitted intensity through a linear polarizer, a key step in many board and competitive exam questions.
3. How is the intensity calculated using Malus law?
Intensity after passing through a polarizer is calculated using:
I = I0 cos2θ
- Measure the angle (θ) between the polarization direction and the polarizer’s axis.
- Square the cosine of that angle.
- Multiply by the initial intensity (I0).
4. What happens at 90 degrees in Malus law?
According to Malus law, at 90° between the polarizer axes, the transmitted intensity becomes zero:
- cos 90° = 0; so I = 0
- No light is transmitted through crossed polarizers.
- This is a frequent exam question demonstrating complete extinction of polarized light.
5. What is Brewster law and Malus law?
Malus law and Brewster law are both concepts in light polarization but describe different phenomena:
- Malus law: Gives intensity of polarized light after passing through a polarizer (I = I0 cos2θ).
- Brewster law: Gives the angle at which reflected light is perfectly polarized (tanθB = n2/n1).
6. What is Malus law formula?
The formula for Malus law is:
I = I0 cos2θ
- Where I0 is the original light intensity, and θ is the angle between the light's polarization direction and the polarizer's axis.
7. How is Malus law used in JEE or NEET exams?
Malus law is frequently asked in JEE Main, Advanced, and NEET exams to:
- Calculate transmitted intensity for given angles and polarizer arrangements.
- Solve conceptual problems about the behavior of polarizers.
- Interpret graphs of intensity versus angle.
8. Does Malus law apply to unpolarized light?
Malus law strictly applies to completely polarized light. For unpolarized light:
- The first polarizer only transmits half the original intensity.
- After the second polarizer, Malus law applies to the already polarized light.
9. Can Malus law be extended for more than two polarizers? How?
Yes, Malus law can be used for multiple polarizers by applying the cos2θ law successively:
- After the first polarizer, intensity is halved for unpolarized light.
- For each subsequent polarizer, use the angle between adjacent polarizer axes: I = Iprevious cos2θ.
- This approach helps calculate transmitted light through any number of polarizers.
10. What is meant by 'cos²θ' in the intensity formula and which angle is it?
In Malus law, cos²θ represents the square of the cosine of the angle between the light’s polarization direction and the axis of the polarizer:
- θ is the angle between the plane of the incoming polarized light and the transmission axis of the polarizer.
- This angle is critical in determining the resultant intensity passed by the polarizer, as shown by the formula I = I0 cos2θ.
11. Why does intensity become zero if the polarizer axes are perpendicular?
When polarizer axes are perpendicular (angle = 90°), the transmitted intensity drops to zero because cos 90° = 0:
- No light passes through crossed polarizers.
- This is called complete extinction, highlighting a key experimental and exam concept.
12. What are common mistakes students make when applying Malus law in numericals?
Common mistakes when using Malus law include:
- Using the law directly for unpolarized light (instead, half the intensity first).
- Confusing the angle θ (must be between polarization direction and polarizer axis).
- Incorrect sequence in multiple polarizer problems.
- Ignoring when I = 0 for perpendicular polarizers.
