
At the first minimum adjacent to the central maximum of a single-slit diffraction pattern the phase difference between the Huygens wavelet from the edge of the slit and the wavelet from the mid-point of the slit is
\[\left( a \right)\]$\dfrac{\pi }{8}radian$
\[\left( b \right)\]$\dfrac{\pi }{4}radian$
\[\left( c \right)\]$\dfrac{\pi }{2}radian$
\[\left( d \right)\]$\pi {\text{ }}radian$
Answer
232.8k+ views
Hint: When we see in single slit diffraction, a line perpendicular to the slit gets superadded. But when we see in double-slit diffraction, the light gets refracted once passing through the slits, to produce an interference pattern on the screen then the light waves commenced from those slits interfere with each other.
Complete step by step Solution:
Suppose there is the screen and there is a single slit placed in front of it. Then there is the distribution of energy on the outlets of the screen. The pattern formed will be in symmetric nature about its axis. Now we have to find the phase difference which should be between the edge of the slit and the wavelet which will be at the midpoint of the slit.
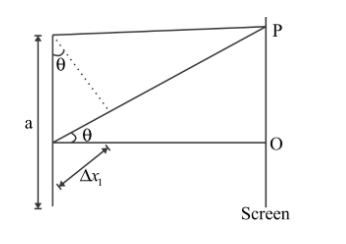
As we already know,
For the first minima at the position P
$ \Rightarrow a\sin \theta = \lambda $
Where $a$will be the length of the slit and $\lambda $will be its wavelength.
So now, phase difference will be calculated and it will be like this
$ \Rightarrow \vartriangle {\lambda _1} = \dfrac{{\vartriangle {x_1}}}{\lambda } \times 2\pi $
As we can see from the figure
$ \Rightarrow \vartriangle {x_1} = \left( {a/2} \right)\sin \theta $
And for first minima in the single-slit diffraction pattern,
$ \Rightarrow a\sin \theta = \lambda $
\[ \Rightarrow \dfrac{a}{2}\sin \theta = \dfrac{\lambda }{2}\]
Now we will put the above value in the $\vartriangle \phi $
$ \Rightarrow \dfrac{{\left( {a/2} \right)\sin \theta }}{\lambda } \times 2\pi $
After solving the above equation, we get
$ \Rightarrow \vartriangle {\phi _1} = \dfrac{\lambda }{{2\lambda }} \times 2\pi $
$ \therefore \pi {\text{ }}radian$
Hence, the option $d$ is the right choice for this question.
Note: Well, single slit diffraction involves sending a beam of light or electrons or alternative objects through one slit, whereas double-slit diffraction involves two slits. With one slim (comparable to the wavelength of the beam) slit, the beam diffracts broadly speaking altogether directions behind the slit and spreads everywhere a downstream viewing screen. With two slim slits, the beams from each slit additionally part generally; however currently the two beams overlap, making an interference pattern at the viewing screen.
Complete step by step Solution:
Suppose there is the screen and there is a single slit placed in front of it. Then there is the distribution of energy on the outlets of the screen. The pattern formed will be in symmetric nature about its axis. Now we have to find the phase difference which should be between the edge of the slit and the wavelet which will be at the midpoint of the slit.

As we already know,
For the first minima at the position P
$ \Rightarrow a\sin \theta = \lambda $
Where $a$will be the length of the slit and $\lambda $will be its wavelength.
So now, phase difference will be calculated and it will be like this
$ \Rightarrow \vartriangle {\lambda _1} = \dfrac{{\vartriangle {x_1}}}{\lambda } \times 2\pi $
As we can see from the figure
$ \Rightarrow \vartriangle {x_1} = \left( {a/2} \right)\sin \theta $
And for first minima in the single-slit diffraction pattern,
$ \Rightarrow a\sin \theta = \lambda $
\[ \Rightarrow \dfrac{a}{2}\sin \theta = \dfrac{\lambda }{2}\]
Now we will put the above value in the $\vartriangle \phi $
$ \Rightarrow \dfrac{{\left( {a/2} \right)\sin \theta }}{\lambda } \times 2\pi $
After solving the above equation, we get
$ \Rightarrow \vartriangle {\phi _1} = \dfrac{\lambda }{{2\lambda }} \times 2\pi $
$ \therefore \pi {\text{ }}radian$
Hence, the option $d$ is the right choice for this question.
Note: Well, single slit diffraction involves sending a beam of light or electrons or alternative objects through one slit, whereas double-slit diffraction involves two slits. With one slim (comparable to the wavelength of the beam) slit, the beam diffracts broadly speaking altogether directions behind the slit and spreads everywhere a downstream viewing screen. With two slim slits, the beams from each slit additionally part generally; however currently the two beams overlap, making an interference pattern at the viewing screen.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




