Question

Assertion: The emf of the driver cell in the potentiometer experiment should be greater than the emf of the cell to be determined.
Reason: The fall of potential across the potentiometer wire should not be less than the emf of the cell to be determined.
(A) Both Assertion and Reason are correct and Reason is the correct explanation for Assertion
(B) Both Assertion and Reason are correct but Reason is not the correct explanation for Assertion
(C) Assertion is correct but Reason is incorrect
(D) Assertion is incorrect but Reason is correct

Answer 1

Hint: If emf of the driver cell in the potentiometer is not greater than the emf of the cell, the fall of potential across the potentiometer wire would not be greater than the emf of the cell to be determined and there will be no balance point.

Complete step by step solution:
In this experiment, we determine the emf of a cell which is not known to us using a potentiometer. A potentiometer has a wire which is generally several meters long. It is stretched between two points A and B on a wooden board. We take two cells with emf’s \[{E_1}{\text{ }}\] and ${E_2}$ out of which one of them is known to us. The positive terminal of \[{E_1}\] is connected to the end A and negative terminal to a jockey and galvanometer.
When a steady current starts flowing through the circuit, we start moving our jockey along wire AB in a way such that the deflection in the galvanometer becomes zero. This is our balance point.

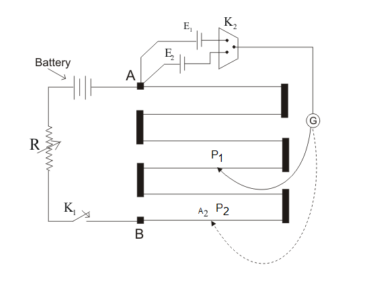
 At this point the potential drop across this particular length of wire balances the emf When a steady current starts flowing through the circuit, we start moving our jockey along wire AB in a way such that the deflection in the galvanometer becomes zero. This is our balance point. At this point the potential drop across this particular length of wire balances the emf \[{E_1}\] that we are supposed to determine. Then we use the formula: \[{E_1} = \dfrac{{{L_1}}}{{{L_2}}}{E_2}\] to determine \[{E_1}\].
However, if the emf of the driving cell (\[{E_2}\]) was not greater than the emf to be determined (\[{E_1}\]), the potential drop across wire AB would also have been lesser than the emf to be determined (\[{E_1}\]) and we would never have obtained a balance point, i.e. \[{L_1}\] or \[{L_2}\].
Therefore, both the Assertion and Reason given in the question are correct and the given Reason is also the correct explanation for the Assertion.

Option (A) is correct.

Note: The basic principle on which a potentiometer works is that the potential drop across the potentiometer wire is directly proportional to its length$ \Rightarrow E \propto L \Rightarrow \dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{{L_1}}}{{{L_2}}} \Rightarrow {E_1} = \dfrac{{{L_1}}}{{{L_2}}}{E_2}$.