Question

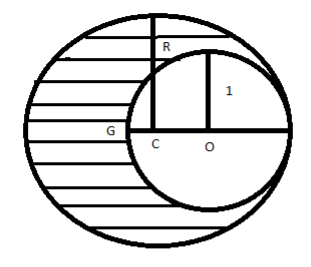
As shown in figure, when a spherical cavity ( Centered at $0$ ) of radius $1$ is cut of a uniform sphere of radius $'R'$ ( Centered at $C$ ), the center of mass of the remaining (shaded) part of the sphere is at $G$ i.e. on the surface of the cavity. $R$ can be determined by the equation.
(A). $\left( {{R^2} + R + 1} \right)\left( {2 - R} \right) = 1$
(B). $\left( {{R^2} - R - 1} \right)\left( {2 - R} \right) = 1$
(C). $\left( {{R^2} - R + 1} \right)\left( {2 - R} \right) = 1$
(D). $\left( {{R^2} + R - 1} \right)\left( {2 - R} \right) = 1$

Answer 1

Hint: Sphere: A sphere is a geometrical object in three dimensional space that is the surface of a ball. Like a circle in two dimensional space, a sphere is defined mathematically as the set of points that are all at the same distance $'r'$ from a given point in a three dimensional space.
Volume of a sphere $ = \dfrac{4}{8}\pi {r^3}$
$r$ is the density is given by
$\operatorname{density} = \dfrac{{\operatorname{mass} }}{{\operatorname{volume} }}$
$\rho = \dfrac{M}{V}$
$\rho = \dfrac{M}{{\dfrac{4}{3}\pi {r^3}}} \Rightarrow M = \dfrac{4}{3}\pi {r^3}\rho $
Centre of mass: This is the point to which a force may be applied to cause a linear acceleration without an angular acceleration. Or A point where the whole mass is supposed to be concentrated.

Complete step by step answer:
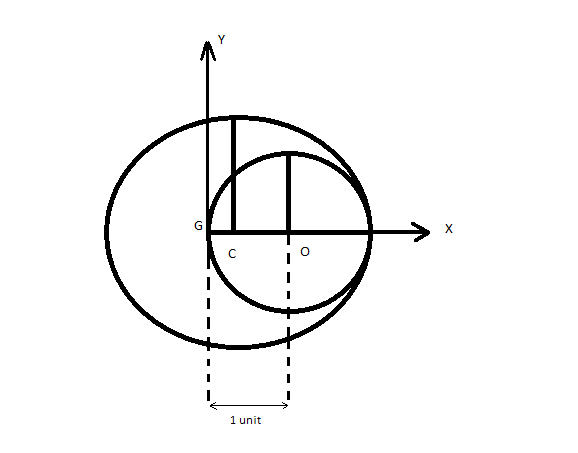
Here, As given $'O'$ is the center of the cavity. $'C'$ is the center of a solid sphere.
So now the modified diagram is


Step 1
Let the origin be at $G$
Now firstly we have to find the mass of solid sphere $\left( {{M_s}} \right)$ which can be found by formula of density
$\rho = \dfrac{{{M_s}}}{{\dfrac{4}{3}\pi {R^3}}}$ = now after the cross multiply
The ${M_s}$ will be ${M_s} = \dfrac{4}{3}\pi {R^3}\rho {{ - - - - - - - - - - }}\left( 1 \right)$
Here now we have to find out the mass of cavity $\left( {{M_c}} \right)$
Again by using the formula of density here we have the mass of the cavity is.
${M_c} = \dfrac{4}{3}\pi {R^3}\rho {{ - - - - - - }}\left( 2 \right)$
Now the radius for the cavity is $1$ unit, so put $R = 1$ in ${2^{nd}}$ equation
${M_c} = \dfrac{4}{3}\pi \rho $
Step.2
Now here we have to find out the center of mass of sphere is
${X_s} = GC$
Which is
${X_s} = 2 - R$
Now here we have to find out the center of mass of the cavity.
${X_c} = 2 \times 1 - 1$
$ \Rightarrow {X_c} = 1$
Now we have to find the common center of mass of the system.
The formula which have to use here
${X_{\operatorname{common} }} = \dfrac{{{M_s}{X_s} + {M_c}{X_c}}}{{{M_s} + {M_c}}}{{ - - - - - - - }}\left( 1 \right)$
${X_{\operatorname{common} }} = $ common center of mass.
Now put the value ${M_s},{X_s},{M_c},{X_c}$ in $\left( 1 \right)$ equation.
${X_{\operatorname{common} }} = \dfrac{{\left( {\dfrac{4}{3}\pi {R^3}\rho } \right) \times \left( {2 - R} \right) + \left( { - \dfrac{4}{3}\pi \rho } \right) \times 1}}{{\dfrac{4}{3}\pi {R^3}\rho + \left( {\dfrac{4}{3}\pi \rho } \right)}}$
Now here system in the state of rest they
${X_{com}} = 0$
$ \Rightarrow 0 = \dfrac{4}{3}\pi {R^3}\rho \left( {2 - R} \right) - \dfrac{4}{3}\pi \rho $
So now proceed further.
$ \Rightarrow \dfrac{4}{3}\pi {R^3}\rho \left( {2 - R} \right) = \dfrac{4}{3}\pi \rho $
Cancel both side few terms
$ \Rightarrow {R^3}\left( {2 - R} \right) = 1$
Now by opening the Bracket.
$ \Rightarrow 2{R^3} - {R^4} = 1$
Now $2{R^3}$ Can be written as ${R^3} + {R^3} = 2{R^3}$
So the above equation will be.
$ \Rightarrow {R^3} + {R^3} - {R^4} = 1$
Taking $'1'$ on L.H.S
$ \Rightarrow {R^3} + {R^3} - {R^4} - 1 = 0$
Now by adjustment we have
$ \Rightarrow \left( {{R^3} - 1} \right) + {R^3} - {R^4} = 0{{ - - - - - - - - }}\left( 2 \right)$
Now
$\left( {{R^3} - 1} \right)$ can be written as $\left( {{R^3} - {1^3}} \right)$ and it is the formula of ${a^3} - {b^3}$
Which is
$ \Rightarrow {a^3} - {b^3} = \left( {{a^2} + {b^2} + ab} \right)\left( {a - b} \right)$
Now $\left( {{R^3} - {1^3}} \right)$ will be
$ \Rightarrow \left( {{R^3} - {1^3}} \right) = \left( {R - 1} \right)\left( {{R^2} + R + 1} \right)$
Now putting in equation $\left( 2 \right)$
$\left( {R - 1} \right)\left( {{R^2} + R + 1} \right) + {R^3} - {R^4} = 0$
From these terms taking $ - {R^3}$ is common.
$\left( {R - 1} \right)\left( {{R^2} + R + 1} \right) - {R^3}\left( {R - 1} \right) = 0$
Now taking $\left( {R - 1} \right)$ common.
$\left( {R - 1} \right)\left( {{R^2} + R + 1 - {R^3}} \right) = 0$
Now here we have the terms
$R - 1 = 0$
$ \Rightarrow R = 1$
And also
${R^2} + R + 1 - {R^3} = 0$
Now adding both sides $'1'$ in the above term.
$ \Rightarrow {R^2} + R + 1 - {R^3} + 1 = 0 + 1$
Now the equation becomes.
${R^2} + R + 1 - {R^3} + 1 = 1$
$ \Rightarrow {R^2} + R + 2 - {R^3} = 1$
Now after factorising it we have the equation.
$\therefore \left( {2 - R} \right)\left( {{R^2} + R + 1} \right),1$
So option ‘A’ is correct.

Note: Few important points about the center of mass:
1. The position of center of mass of a system is independent of the choice of coordinate system.
2. The position of the center of mass depends on the shape and size of the body.
3. The concept of center of mass proves that the laws of mechanics, which are true for a point mass, are equally valid for all macroscopic bodies.
4. If we know the center of mass of different parts of the system and their masses, we can get the combined center of mass by beating various parts as point objects whose masses are concentrated as their respective center of mass.