Question

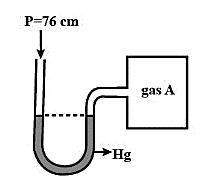
An open-ended mercury manometer is used to measure the pressure exerted by a trapped gas as shown in the figure. Initially, manometer shows no difference in mercury level in both columns as shown in the diagram.
After sparking, ‘A’ dissociates according to the following reaction:
$A(g)\to B(g)+3C(g)$
If the pressure of gas ‘A’ decreases to $0.9atm$. Then:
(assume temperature to be constant and is 300K)

This question has multiple correct options.
(A) total pressure increased to $1.3atm$
(B) total pressure increased by $0.3atm$
(C) total pressure increased by $22.3\,cm\,of\,Hg$
(D) the difference in mercury level is $228\,mm$

Answer 1

Hint: The manometer is a device which measures the pressure exerted by the trapped gas in the container, that is seen through the rise in the mercury level in the two vertical columns. As the pressure increases, it causes the mercury level to rise.

Complete step by step solution:
It is given that in the system, the atmospheric pressure, ${{P}_{i}}=76\,cm\,=1\,atm$. Since initially no pressure is exerted by the gas A trapped in the container and the level of mercury is equal in both the columns. The pressure of gas A is also equal to the atmospheric pressure and the pressure from gas B and C is zero initially.
But as given, on sparking the pressure of gas A decreases to $0.9atm$. Then, the difference in pressure of gas A will be $(initial\,pressure-final\,pressure)=1-0.9=0.1\,atm$.
Let the decrease in the pressure be X.
As the reaction follows: $A(g)\to B(g)+3C(g)$
The pressure of gas A decreases to $1-X=0.9\, atm$.
The pressure of gas B is $X=0.1\,atm$ and pressure of gas C is $3X=3\times 0.1=0.3\,atm$ .
Then, the total pressure exerted within the system, ${{P}_{t}}=(1-X)+X+3X=1.3atm$.
So, we get the increase in the pressure of the system due to gas A undergoing sparking, causing the mercury level to rise in the column.
Thus, total pressure is increased by$\Delta P={{P}_{t}}-{{P}_{i}}=1.3-1=0.3\,atm$
$=0.3\times 76\,cm\,for\,Hg$
$=0.3\times 760\,mm\,=228\,mm\,for\,Hg\,$
This increase in the total pressure of the system, $\Delta P$ is proportional to the difference in mercury level.

Therefore, in the manometer it is seen that there is option (A)- total pressure increased to $1.3atm$, option (B)- total pressure increased by $0.3atm$ and option (D)- the difference in mercury level is $228\,mm$.

Note: The height between the mercury levels in the two columns corresponds to the difference in the pressure exerted by the gas in the container and the atmosphere. Similarly, depending on the pressure of the system the height of mercury in adjacent tubes rises.