Question

An electron moving with a uniform velocity along the positive $x-$direction enters a magnetic field directed along the positive $y-$direction. The force on the electron is directed along
A. Positive $y-$direction
B. Negative $y-$direction
C. Positive $z-$direction
D. Negative $z-$ direction

Answer 1

Hint: When an electron is moving along the $x-$direction, it enters a magnetic field directed along the positive$y-$direction. If an $x-$axis and $y-$axis are perpendicular to each other, then the direction of the magnetic force acting on the particle is given by Fleming’s left-hand thumb rule.




Formula used:
The radius,$R$ of the circular path in a magnetic field,$B$can be expressed in the following way:
$R=\dfrac{mv}{qB}$
Here $m\And v$are the mass and velocity of the particle with charge $q$.


Complete answer:

Consider the unit vectors in $x,y\And z$ the direction be $\hat{i},\hat{j}\And \hat{k}$. Since it is given, the charged particle moves along $x-$ direction with a uniform velocity and the magnetic field $\vec{B}$along $y-$ direction.

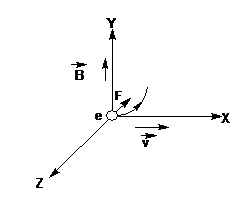
When a particle carrying charge$q$, moving with uniform velocity $\vec{v}$enters into a magnetic field $\vec{B}$, it experiences a magnetic force,$\vec{F}=q(\vec{v}\times \vec{B})$
$\therefore \vec{F}=q(v\hat{i}\times B\hat{j})$
$\vec{F}=-e(v\hat{i}\times B\hat{j})$
$\vec{F}=evB(-\hat{k})$
Hence the force acting on the electron is directed along the negative $z-$direction.
The overall phenomena can be better understood by Fleming’s left-hand thumb rule.
 This rule tells us if we stretch our index, middle finger, and thumb in such a way that they are mutually perpendicular to each other, the index finger points the direction of the magnetic field along $y-$ the direction and the middle finger shows the direction of current along $x-$the direction, then the thumb will point the subsequent direction of the magnetic force along the positive $z-$direction.

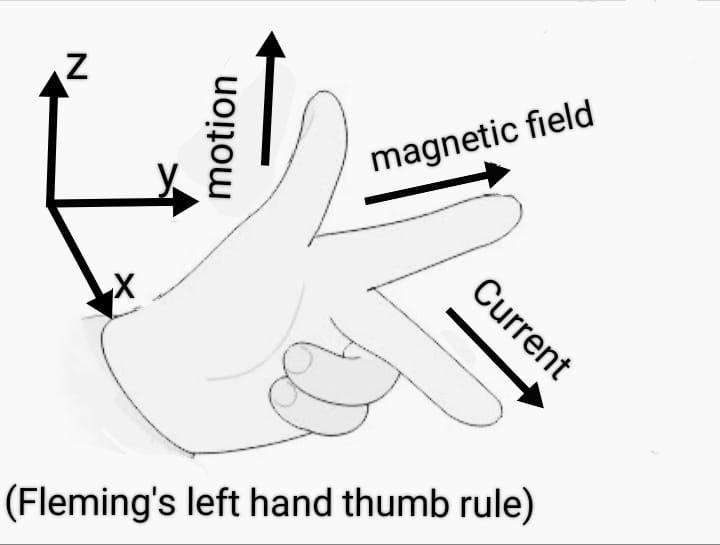
But here the particle is a negatively charged electron, magnetic force acts along the negative $z-$direction.

Thus, option (D) is correct.


Note:Protons and electrons both are particles with same charge, when they move in the magnetic field , will experience the same magnitude of magnetic force but in the opposite direction. As we know the mass of an electron is less than that of a proton hence the electron will get deflected by a higher degree than the proton.