Question

An electron is moving along +x direction with a velocity of $6 × 10^6\,ms^{–1}$. It enters a region of the uniform electric field of 300 V/cm pointing along +y direction. The magnitude and direction of the magnetic field set up in this region such that the electron keeps moving along the x-direction will be
A. \[3 \times {10^{ - 4}}{\rm{ T}}\], along –z direction
B. \[5 \times {10^{ - 3}}{\rm{ T}}\], along –z direction
C. \[5 \times {10^{ - 3}}{\rm{ T}}\], along +z direction
D. \[3 \times {10^{ - 4}}{\rm{ T}}\], along +z direction

Answer 1

Hint:Suppose any charge q is moving in the direction of the positive x- axis with velocity v. Because of charge moving an electric field exists around it. This electric field will apply a force on the charge whose magnitude will be qE in the direction that depends on the nature of the charge. If you assume the charge as positive. The electric field is trying to change the direction of the charge as it applies a force. To set up a magnetic field in the region to stop the direction of the charge. The net force must be in the opposite direction of the electric field.

Formula used
Force due to electric field,
\[{F_e} = q\overrightarrow E \]
Force due to magnetic field ,
\[{F_m} = q\overrightarrow {{\rm{ }}v} \times \overrightarrow B \]
In cross product, \[\widehat i \times \overrightarrow k = - \widehat j\]

Complete step by step solution:
Given velocity is along +x direction and the uniform electric field of 300 V/cm pointing along +y direction.

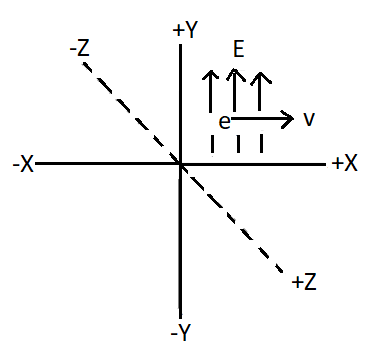
Image: Three dimensions of charge e moving

To calculate the direction of the magnetic field:
Force due to electric field is applied in the direction of \[\widehat j\],
\[{F_e} = q\overrightarrow E \]
Force due to the magnetic field must be in the opposite direction of the same magnitude as \[ - \widehat j\] ,
\[{F_m} = q\overrightarrow {{\rm{ }}v} \times \overrightarrow B \]
Thus
\[\begin{array}{l}\overrightarrow v \times \overrightarrow B = - \widehat j\\\widehat i \times \overrightarrow B = - \widehat j\\\widehat i \times \overrightarrow B = \widehat i \times \widehat k\\\overrightarrow B = \widehat k\end{array}\]
Therefore the direction of the magnetic field set up in this region will be along +z direction.

To calculate the direction of magnetic field:
Equating the magnitude as
\[{F_m} = {F_e}\]
\[qvB = qE\] (The charge of electron must be canceled)
Given velocity = $6 × 10^6\,ms^{–1}$
uniform electric field = 300 V/cm = \[3 \times {10^4}V/m\]
Substituting the value, we get
\[B = 5 \times {10^{ - 3}}T\]
Therefore the magnitude of the magnetic field set up in this region is \[B = 5 \times {10^{ - 3}}T\].

Hence option C is the correct answer.

Note: A Moving electron produces a magnetic field around it. Electric fields and magnetic fields are also known as electromagnetic fields or simply EMF. Which consist of waves of electric and magnetic energies moving together.