Question

A uniform chain of length 2m is kept on a table such that a length of 60cm hangs freely from the edge of the table. The total mass of the chain is 4kg. What is the work done in pulling the entire chain on the table?
A. 7.2 J
B. 3.6 J
C. 120 J
D. 1200 J

Answer 1

Hint: The principle of conservation of energy says that energy can neither be created nor be destroyed. But in order to increase the potential energy of the system, some external agent must do some work which will increase the potential energy of the system. Potential energy is the energy associated with the height or altitude.

Formula used:
$\Delta U = mgh$, where $\Delta U$ is the increase in potential energy of mass ‘m’ after going up by height ‘h’.

Complete step-by-step solution:
An increase in the potential energy of the system in a uniform body is equivalent to the increase in the internal energy of the center of mass of the system. In this question, we have to focus on two parts of the chain: the hanging one and lying on the table. The part lying on the table has a fixed altitude i.e. its height won’t change. Hence there’s no contribution of the part lying on the table in increasing the potential energy. Coming to the hanging part:
Given the length of the hanging part = 60cm or 0.6m

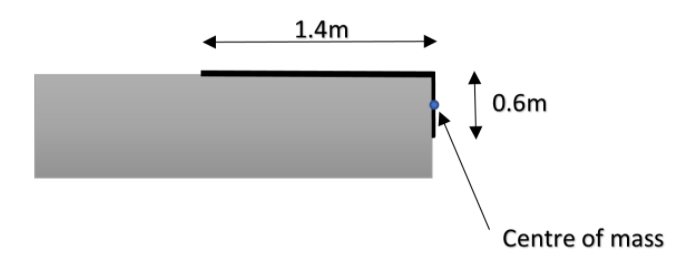
The linear mass density $(\lambda )$of the chain is = $\dfrac{total \ mass \ of \ chain}{total\ length\ of\ chain} = \dfrac42 = 2\ kgm^{-1}$
Hence the mass of the hanging part will be = $\lambda \times \ length \ of\ hanging\ part$
= $2 \times 0.6 = 1.2 kg$
Now, the center of mass of the hanging part will be in the middle of the hanging part, as it is a uniform chain. Hence height of centre of mass from the table = $\dfrac {0.6}{2} = 0.3\ m$
Now, after pulling the chain completely on the table, the center of mass of the hanging part will also get elevated by 0.3 m as the rest of the chain. So, the increase in potential energy:
 $\Delta U = m g h = 1.2 \times 10 \times 0.3 = 3.6\ J$
Hence the external agent must do the work of 3.6 J. So the option (B) is the correct answer.

Note: In such a question we have to focus on many breakpoints. Like if the chain were not uniform, we have to solve it by integration. If there is friction on the table, we might have proceeded by drawing a free body diagram of the chain. Here we’ve used the principle of conservation of mechanical energy as the reason for the increase in internal energy is the work done by an external agent.