Question

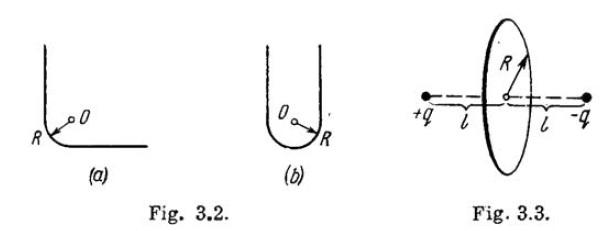
A thread carrying a uniform charge \[\lambda\] per unit length has the configurations shown in Fig. a and b. Assuming a curvature radius R to be considerably less than the length of the thread, find the magnitude of the electric field strength at the point O.

Answer 1

Hint: Before starting this question, we should know about electric field. Each location in space where a charge exists in any form can be considered to have an electric field attached to it. The electric force per unit charge is another name for an electric field.

Complete answer:
Finding $Ex$ and $Ey$ viz. the projections of $\vec{E}$ in Fig, where it is assumed that$\lambda >0$, solves the problem.

Let's begin with $E_x$. The charge element of the segment $dx$ contributes to $E_x$ in the following manner:
$d{{E}_{x}}=\dfrac{1}{4\pi {{E}_{0}}}\dfrac{\lambda dx}{{{r}^{2}}}\sin \alpha ......(1)$

Let's condense this phrase into a form that will allow for easy integration. In this instance $dx=\dfrac{rd\alpha }{\cos \alpha }$, and $r=\dfrac{y}{\cos \alpha }$. Then
$d{{E}_{x}}=\dfrac{\lambda }{4\pi {{E}_{0}}y}\sin \alpha d\alpha $

Using this expression's integration over between 0 and π/2, we discover
${{E}_{x}}=\dfrac{\lambda }{4\pi {{E}_{0}}y}$

Remembering that $d{{E}_{y}}$differs from $d{{E}_{x}}$in that $\sin \alpha $ in (1) is only replaced by $\cos \alpha $ will help you locate the projection Ey.
This gives
$d{{E}_{y}}=\dfrac{(\lambda \cos \alpha d\alpha )}{4\pi {{E}_{0}}y}$ and${{E}_{y}}=\dfrac{\lambda }{4\pi {{E}_{0}}y}$

We have discovered an intriguing outcome:
${{E}_{x}}={{E}_{y}}$independent of y,
Specifically, $\vec{E}$is ${{45}^{o}}$degrees away from the rod. The value of $\vec{E}$ modulus is
$E=\sqrt{E_{x}^{2}+E_{y}^{2}}=\lambda \sqrt{2/4\pi {{E}_{0}}y}$

At point O, the thread's straight sections have no effect on the electric field there, which is equal to zero. Let's compute the field strength at the centre of an arc of radius R and linear charge density and which subtends angle ${{\theta }_{0}}$at the centre to get a generic expression for the curved part (arc).

The sought-after field strength will be determined by the symmetry and will be directed along the angle${{\theta }_{0}}$ bisector, which is provided by
$E=\int\limits_{-{{\theta }_{0}}/2}^{+{{\theta }_{0}}/2}{\dfrac{\lambda R(d\theta )}{4\pi {{E}_{0}}{{R}^{2}}}\cos \theta }$
$=\dfrac{\lambda }{2\pi {{E}_{0}}R}\sin \dfrac{{{\theta }_{0}}}{2}$

The field strength due to the rotated component at the position
${E}'=\dfrac{\sqrt{2}\lambda }{4\pi {{E}_{0}}R}$ is likewise the desired result in our case where ${{\theta }_{0}}=\pi /2$.

(b) The field strength due to the specified curved component (semi-circle) at the point O becomes $\dfrac{\lambda }{2\pi {{E}_{0}}R}$ and is directed vertically upward whereas the net field strength at O owing to straight parts equals $\sqrt{2}\left( \dfrac{\sqrt{2}\lambda }{4\pi {{E}_{0}}R} \right)=\dfrac{\lambda }{2\pi {{E}_{0}}R}$ and is directed vertically down.
Thus, the desired net field strength is zero.

Note: Electric charge or magnetic fields with variable amplitudes can produce an electric field. The attraction forces that keep together atomic nuclei and electrons at the atomic scale are brought on by the electric field.