Question

A tangential force $2N$ acts at the rim of a ring of radius $15m$ and causes the ring to turn through an angle $60^\circ $ the work done by the force will be:
A) $5\pi $
B) $10\pi $
C) $15\pi $
D) $20\pi $

Answer 1

Hint: A power which follows up on a moving body toward a digression to the way of the body, its impact being to increment or lessen the speed; - recognized from an ordinary power, which acts at right points to the digression and alters the course of the movement without changing the speed.
Net force implies ascertaining the subsequent force from n diverse contributing powers.
In material science and mechanics, force is what might be compared to direct power. It is likewise alluded to as the occasion, snapshot of power, rotational power, or turning impact, contingent upon the field of study.

The idea began with the investigations by Archimedes of the use of switches.
Force is a proportion of the power that can make an item pivot about a hub.
Similarly, as power is the thing that makes an article quicken in direct kinematics, force is the thing that makes an item gain precise speeding up.
Force is a vector amount.

Formula used:
The formula of torque $T$ is
$\overrightarrow T = \overrightarrow r \times \overrightarrow F $
$\overrightarrow F $= force, $\overrightarrow r $ = the lever arm and
The angle $\theta $, between the lever arm $r$ and force $F$ is known, the magnitude of the torque can be calculated as $\overrightarrow T = \overrightarrow r \times \overrightarrow F \sin \theta $

Complete step by step answer:



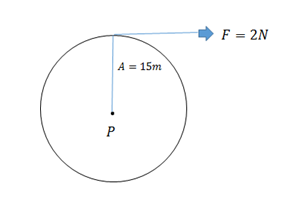
Let A tangential force $2N$, radius $15m$, an angle $60^\circ $
Net torque, $\overrightarrow T = \overrightarrow r \times \overrightarrow F $
$ \Rightarrow 15m\mathop j\limits^ \wedge \times 2N\mathop i\limits^ \wedge $
$ \Rightarrow 30Nm$
Since, we already know that $\left( {\because \sin 60^\circ = \dfrac{\pi }{3}} \right)$ $\left( {\because \overrightarrow T = 30Nm} \right)$ $\left( {\because \sin 60^\circ = \dfrac{\pi }{3}} \right)$
Work done,
$W = \overrightarrow T \times \Delta \overrightarrow \theta $
$ \Rightarrow W = 30 \times \dfrac{\pi }{3}$
$ \Rightarrow W = 10\pi $

Hence the answer is $\left( B \right)$

Note: A surface containing the essential foci of focuses in a plane opposite to the optical hub of an astigmatic framework. Spiral power by and large methods a power applied an outspread way towards the middle or away from the middle. In outward siphons, spiral power (additionally outspread push) is the term used to assign the power following up on the siphon rotor. The extraneous increasing speed is a proportion of the pace of progress in the size of the speed vector, for example, speed, and the typical increasing speed is a proportion of the pace of altering the course of the speed vector.