Question

A straight line is equally inclined to all the three axes. Then the angle made by y-axes is
$
  {\text{A}}{\text{.}}{\cos ^{ - 1}}\left( {\dfrac{1}{3}} \right) \\
  {\text{B}}{\text{.}}{\cos ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right) \\
  {\text{C}}{\text{.}}{\cos ^{ - 1}}\left( {\dfrac{2}{{\sqrt 3 }}} \right) \\
  {\text{D}}{\text{.}}\dfrac{\pi }{4} \\
$

Answer 1

Hint : Use the concept of direction cosines i.e. make the sum of squares of all the direction cosines as equal to one.


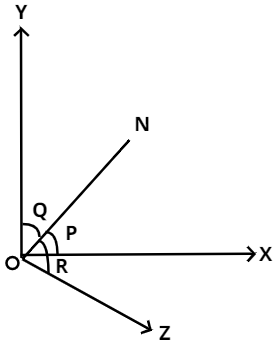
This the diagram of the line equally inclined to all the three axes.
From the Figure we come to know that ON is the line which is equally inclined to all the three axes.
Here we will use the concept of direction cosines $l,m,n$.
From the figure we know
$
  l = \cos p{\text{ }}......{\text{(}}i{\text{)}} \\
  m = \cos q\,\,\,\,\,\,\,\,\,\,\,\,......(ii) \\
  n = \cos r\,\,\,\,\,\,\,\,\,\,\,\,\,......(iii) \\
    \\
$
We also know ${l^2} + {m^2} + {n^2} = 1\,\,\,\,\,\,......(iv)$
From the question we come to know $p = q = r = \theta (say)\,\,\,\,\,\,......(v)$
From ${\text{(}}i{\text{),(}}ii{\text{),(}}iii{\text{),(}}iv{\text{)\& (}}v{\text{)}}$We do
 ${\cos ^2}\theta + {\cos ^2}\theta + {\cos ^2}\theta = 1$
$ \to 3{\cos ^2}\theta = 1$
Therefore,
$\cos \theta = \dfrac{1}{{\sqrt 3 }}$
Then ,
$\theta = {\cos ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right)$
Hence the correct option is B.

Note :- In these types of questions we will always use the concept of cosines . That is the sum of squares of all the direction cosines is one. By using this we can get the answer easily . Drawing figures will make your concept more clear.