Question

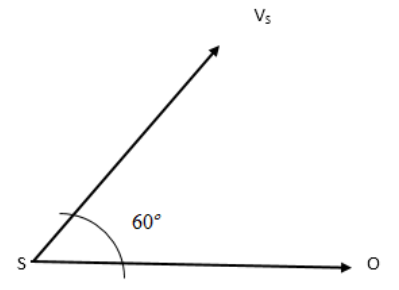
A source of sound S emitting waves of frequency \[100Hz\] and an observer O are located at some distance from each other. The source is moving with a speed of \[19.4m{s^{ - 1}}\] at an angle of \[{60^o}\] with the source observer line as shown in the figure. The observer is at rest. The apparent frequency observed by the observer is: (Velocity of sound in air is \[330m{s^{ - 1}}\])

A) \[97Hz\]
B) \[100Hz\]
C ) \[103Hz\]
D) \[106Hz\]

Answer 1

Hint:We need to apply Doppler’s effect to get the value of apparent frequency.
Since the source is moving with a certain velocity and inclined to the source-observer line at a certain angle we can find the magnitude of source velocity.
Putting them in the equation of apparent frequency we can obtain the required value.

Complete step-by-step solution:
In the question, it is given that the source approaches the observer, therefore, we can say that the frequency must be more than source frequency. Here, the frequency must be more than \[100Hz\].
So, Option (A) must be incorrect.

Now, let us apply Doppler’s effect to obtain the value of apparent frequency.
We know, using the formula for Doppler’s effect we can find the apparent velocity if we have the values of observer velocity, source velocity and source frequency.
Let:
\[{V_o}\] Be the observer velocity \[{V_{}}\]
\[{V_S}\] Be the Source velocity
\[F\] Frequency of the source
\[f\] Apparent frequency
 Be the speed of light
\[{v_s}\] Magnitude of velocity along SO line
The following data is given in the question:
\[{V_s} = 19.4m{s^{ - 1}}\]
\[F = 100Hz\]
Applying the concept for Trigonometry, we can find the component of \[{V_s}\] that moves along the SO lines such that:
\[{v_s} = {V_s}\cos {60^o}\]
This gives us:
\[{v_s} = 19.4\cos {60^o}\]
Thus, we obtain:
\[{v_s} = 9.7m{s^{ - 1}}\]
Now, applying the formula, we get:
\[f = F(\dfrac{{V - {V_o}}}{{V - {v_s}}})\]
Since, the source is moving, the observer is at rest.
Therefore, \[{V_o} = 0\]
Now, putting the values, we get:
\[f = 100(\dfrac{{330 - 0}}{{330 - 9.7}})\]
On solving, we get:
\[f = 103Hz\]
This is the required answer.

Therefore, option (C) is correct.

Note:We know from Doppler’s effect, there is an upward shift in the perceived frequency as the source moves towards the observer, thus the frequency increases. On the other hand, if the observer moves towards the source, there is a decrease in frequency.
This change in frequency from that of the actual frequency as perceived by the observer is referred to as apparent frequency.