Question

A solid cylinder rolls without slipping down a ${30^ \circ }$ slope. The minimum coefficient of friction needed to prevent slipping, will be:
A) $0.192$
B) $0.18$
C) $0.15$
D) $0.2$

Answer 1

Hint: The cylinder is rolling on a slope, as the given problem the cylinder is rolling, torque will be acting on the cylinder. This torque has a tendency to roll the cylinder and friction being an opposing force will oppose this rolling motion. The torque due friction must be balanced with the torque due to the weight of the cylinder. As no external force is acting on the cylinder, all the force acting on the cylinder must be balanced.

Complete step by step solution:
We are given that a cylinder is rolling on an inclined plane having slope of ${30^ \circ }$ . The surface of the inclined slope has friction. Friction by its nature is an opposing force, it will act in the opposite direction to the motion of the cylinder. Let us first draw the free body diagram of the system and label the forces acting on the solid cylinder.

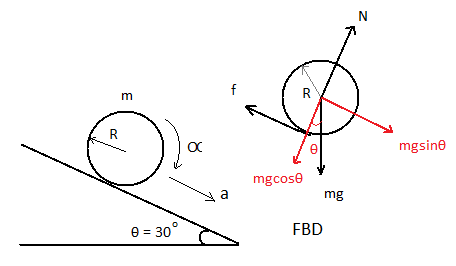
From the diagram, let the mass of the cylinder be $m$ and the radius be $R$ . $\theta $ is the angle of inclination of the slope which is given as $\theta = 3{0^ \circ }$ .
The force due to acceleration due to gravity is $mg$ , we have taken components of this force along the incline and in the direction opposite to the normal force.
$N$ is the normal force acting on the cylinder due to the surface of the inclined. $f$ is the frictional force acting on the cylinder. $\alpha $ is the angular acceleration of the cylinder.
From the diagram we have weight of block along normal to the plane is:
$W = N = mg\cos {30^ \circ }$-----equation $1$
The cylinder will roll in the downward direction, let the linear acceleration along the inclined be $a$ . The forces along the inclined will be:
$mgsin{30^ \circ } - f = ma$------equation $2$
Now, as the block will perform rolling motion, torque is responsible for this rolling motion. This torque will be given as:
$\tau = fR = I\alpha $
Here, $I$ is the moment of inertia of the cylinder. The moment of inertia of the cylinder along its axis of rotation is $I = \dfrac{{m{R^2}}}{2}$
Substituting this value in the above equation, we get:
$fR = \dfrac{{m{R^2}}}{2}\alpha $
$ \Rightarrow f = \dfrac{{mR}}{2}\alpha $
The relation between angular acceleration and linear acceleration $a$ is $a = R\alpha $ .
$ \Rightarrow f = \dfrac{{mR}}{2}\dfrac{a}{R}$
$ \Rightarrow f = \dfrac{{ma}}{2}$-------equation $3$
$ \Rightarrow a = \dfrac{{2f}}{m}$
Substituting this value in equation $2$ , we get
$mgsin{30^ \circ } - f = ma$
$ \Rightarrow mgsin{30^ \circ } - \dfrac{{ma}}{2} = ma$
$ \Rightarrow mg\left( {\dfrac{1}{2}} \right) = \dfrac{{3ma}}{2}$
$ \Rightarrow a = \dfrac{g}{3}$
Substituting this value in equation $3$ , we get
$f = \dfrac{{ma}}{2}$
$f = \dfrac{{ma}}{2} = \dfrac{m}{2} \times \dfrac{g}{3}$
$ \Rightarrow f = \dfrac{{mg}}{6}$
Frictional force is given as $f = \mu N$ , $\mu $ is the coefficient of friction.
From the figure we have achieved that: $N = mg\cos {30^ \circ }$ , therefore, we can have:
$f = \mu N = \mu mg\cos {30^ \circ }$
$ \Rightarrow \dfrac{{mg}}{6} = \mu mg\dfrac{{\sqrt 3 }}{2}$ as $\cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2}$
$ \Rightarrow \mu = \dfrac{2}{{6\sqrt 3 }}$
$ \Rightarrow \mu = 0.192$
Therefore, the minimum coefficient of friction needed to prevent slipping, will be $\mu = 0.192$.

Option A is the correct option.

Note: Frictional force is opposing in nature. The forces on the cylinder must be balanced along the inclined and along the normal to the plane. The moment of inertia of a solid cylinder along its axis of rotation is given as $I = \dfrac{{m{R^2}}}{2}$ . The relation between linear acceleration and angular acceleration is given as $a = R\alpha $ . The components of forces must be taken properly.