Question

A solid cylinder of mass M and radius 2R is rolled up on an incline with the help of planks of mass 2M as shown in the figure.

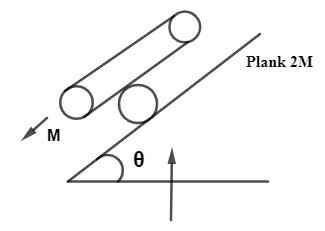
A force (constant) F is acting on the plank parallel to incline. There is no slipping at any of the constant. The friction force between the plank and cylinder is given by
A. $\dfrac{F}{5}$
B. $\dfrac{{3F + 29Mg\sin \theta }}{{57}}$
C. $\dfrac{{3F + 2Mg\sin \theta }}{{19}}$
D. Coefficient of friction value is not given and hence cannot be found.

Answer 1

Hint:Here in this question, we must know that the force of static friction will be $Mg\sin \theta $ if the object on the incline is not moving. The force of kinetic friction will be equal to $Mg\sin \theta $ . if the sloped object is moving but not speeding up.

Formula Used:
Acceleration will be equal to, $a = \alpha .2R$ or we can also write it as, $a = 2\alpha R$.
Where $\alpha $ is alpha(angular acceleration of solid cylinder) here and $R$ stands for the radius of the cylinder.
$I = \dfrac{{MR_0^2}}{2}$

Complete step by step solution:
For point a we know the acceleration will be, using free body diagram we have,

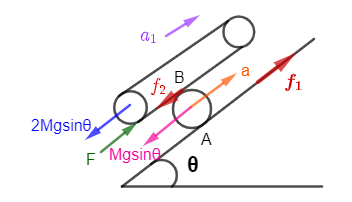
$a = 2\alpha R$
And for point b, the acceleration will be,
${a_1} = 4\alpha R$
As form above both equations we can say that,
$a = \dfrac{{{a_1}}}{2}$
Now, the force acting on the plank, the force equation will be,
$F - 2Mg\sin \theta - {f_2} = 2M{a_1}.....(i)$
Here in the above equation we get the value of force acting on the plank, now we calculate the force acting the cylinder,
$I = \dfrac{{MR_0^2}}{2}$
As we get the equation of moment of inertia for cylinder, now solving it further for the equation we get, as $\therefore {R_0} = 2R$
$I = 2M{R^2}$

Now for the force acting on the cylinder, we get that,
${f_1} + {f_2} - Mg\sin \theta = Ma$
We can also write it as,
${f_1} + {f_2} - Mg\sin \theta = Ma = \dfrac{{M{a_1}}}{2} .....(ii)$
Now we can consider, the moment of force about the centre of the cylinder,
${f_2} \times 2R - {f_1} \times 2R = I\alpha $
Now putting the values of alpha and taking common we get the resultant equation as,
$({f_2} - {f_1}) \times 2R = 2M{R^2} \times \dfrac{{{a_1}}}{{4\alpha }}$
By completing the calculation of the above equation, we get that,
$({f_2} - {f_1}) = \dfrac{{M{a_1}}}{a}.....(iii)$
Using equation(iii) & (ii) we get,
$2{f_2} - Mg\sin \theta = \dfrac{{3M{a_1}}}{4}$

Now by rearranging the values we get the final equation as for it is,
$M{a_1} = \left( {\dfrac{{8{f_2} - 4Mg\sin \theta }}{3}} \right)$
Now using $M{a_1}$ ‘s value in equation(i) we get,
$F - 2Mg\sin \theta - {f_2} = 2M\left( {\dfrac{{8{f_2} - 4Mg\sin \theta }}{3}} \right)$
Now by simplifying the above equation, we get the value as,
$3F - 6Mg\sin \theta - 3{f_2} = 16{f_2} - 8Mg\sin \theta $
Here from above equation, we need the value of ${f_2}$ , so taking ${f_2}$ at one side we get the equation as,
${f_2} = \left( {\dfrac{{3F + 2Mg\sin \theta }}{{19}}} \right)$
From the whole conclusion we get the friction force between the plank and cylinder is $\left( {\dfrac{{3F + 2Mg\sin \theta }}{{19}}} \right)$ .
Therefore, the correct answer of the friction force is $\left( {\dfrac{{3F + 2Mg\sin \theta }}{{19}}} \right)$ .

Hence, the correct option is C.

Note: The normal interaction between the two surfaces under consideration as well as the surface's makeup determine it. Frictional forces are produced by intermolecular interactions between the substances. In all contact, it lessens the relative motion between two bodies or surfaces.