Question

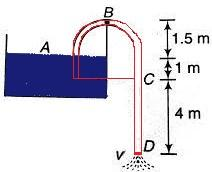
A siphon tube is discharging a liquid of specific gravity 0.9 from a reservoir as shown in the figure to find the pressure at the highest point B.

Answer 1

Hint: Here we have to use Bernoulli's equation; the equation is based upon the principle of conservation of energy. It states that the total energy that is related with a flowing fluid remains constant. The energy related with the flowing fluid is potential energy, kinetic energy and pressure. Here to find out the pressure at the highest point B one has to equate pressure at point A to pressure at point B.

Formula used:
$P + \dfrac{1}{2}\rho {v^2} + \rho gh = {\text{constant}}$ ;
P = Pressure;
$\rho $= Relative density or specific gravity (0.9);
g = Gravitational Constant;
h = Height;
v = Velocity.

Complete step by step solution:
Equate the Bernoulli’s equation for two points A and D, Find v
${P_A} + \dfrac{1}{2}\rho {v^2} + \rho gh = {P_D}$;
Here ${P_A}$ and ${P_D}$ are atmospheric pressure which is $1.01 \times {10^5}$Pa.
${P_A} + \dfrac{1}{2}\rho {v^2} + \rho gh = {P_D} + \dfrac{1}{2}\rho {v^2} + \rho gh$;
Here ${P_A}$ and ${P_D}$ are equal, they will cancel out,
$\dfrac{1}{2}\rho {v^2} + \rho gh = \dfrac{1}{2}\rho {v^2} + \rho gh$;
Put the given values in the above equation
$\dfrac{1}{2}\rho {v^2} + \rho g \times 5 = \dfrac{1}{2}\rho {v^2} + \rho g \times 0$;
At point A there will be no velocity in the liquid , v = 0;
$\rho g \times 5 = \dfrac{1}{2}\rho {v^2}$
Here the relative densities are equal as the liquid is same,
$g \times 5 = \dfrac{1}{2}{v^2}$;
Solve,
$g \times 5 \times 2 = {v^2}$;
$v = \sqrt {10g} $ ;
$v = \sqrt {9.8 \times 10} $ ;
$v = 9.9{\text{ m/s}}$ ;
Now, equate the Bernoulli’s equation at point A and at point B,
${P_A} + \dfrac{1}{2}\rho {v^2} + \rho gh = {P_B} + \dfrac{1}{2}\rho {v^2} + \rho gh$;
Put the values in the above equation,
${P_A} + \dfrac{1}{2}\rho \times 0 + \rho g \times 0 = {P_B} + \dfrac{1}{2}\rho {v^2} + \rho g(1 \cdot 5)$;
Simplify the above equation,
${P_A} + 0 + 0 = {P_B} + \dfrac{1}{2}\rho {v^2} + \rho g(1 \cdot 5)$;
Here,${P_A} = {P_o}$, Put value $1.01 \times {10^5}$Pa.
$1.01 \times {10^5} = {P_B} + \dfrac{1}{2} \times 900 \times {(9.9)^2} + 900 \times 9 \cdot 8 \times 1 \cdot 5$
Take ${P_B}$ to LHS and the rest to RHS and solve,
${P_B} = 1.01 \times {10^5} - \dfrac{1}{2} \times 900 \times {(9.9)^2} - 900 \times 9 \cdot 8 \times 1 \cdot 5$;
Do the necessary calculation,
${P_B} = 4.36 \times {10^4}{\text{ Pa}}$;

Pressure at the highest point B is ${P_B} = 4.36 \times {10^4}{\text{ Pa}}$.

Note: Here we have to first equate point A and D by using the Bernoulli’s equation and find out the velocity and after that to find out the pressure at the highest point B we have to equate the Bernoulli’s equation at point A and B.