Question

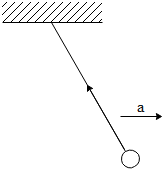
A simple pendulum is oscillating without damping. When the displacement of the bob is less than maximum, its acceleration vector $\vec a$ is correctly shown in:

(A)

(B)

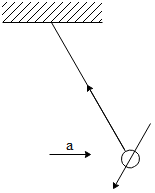
(C)

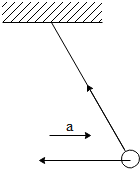
(D)

Answer 1

Hint The simple pendulum is known to us as a pendulum which consists of a mass m hanging from a string which has a length of L and is fixed at a pivot point P. Whenever the pendulum is displaced to an initial angle and is released, the pendulum will swing back and forth with a periodic motion. Based on this concept we have to solve this question.

Complete step by step answer
We know that the bob has both radial as well as tangential acceleration when it is at a displacement less than its maximum displacement.
Let us draw the figure:

From the figure,

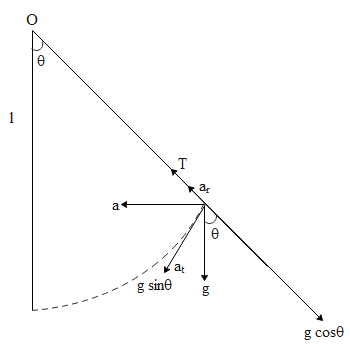
${a_t} = g\sin \theta$and,
${a_r} = \dfrac{T}{m} - g\cos \theta$
The resultant acceleration $\vec a = {\vec a_r} + {\vec a_t}$ points in the direction as shown in the figure

NoteDamping, as we know, is defined as the restraining of the vibratory motion, such as mechanical oscillations, noise or even alternating currents, by the dissipation of energy. IN case of waves, a damped wave is one whose amplitude of oscillation decreases with the time and ultimately goes to zero.