Question

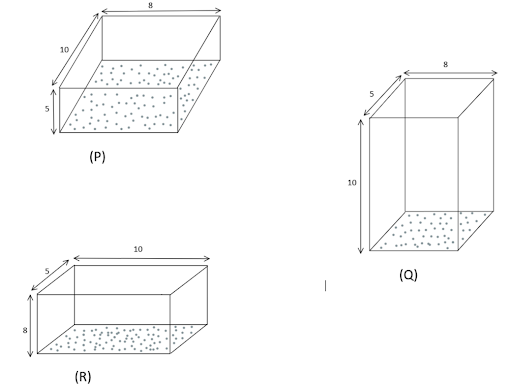
A rectangular block of size $10cm \times 8cm \times 5cm$ is kept in three different positions P, Q and R in turns as shown in the figure. In case, the shaded area is rigidly fixed and a definite force F is applied tangentially to the opposite face to deform the block. The displacement to the upper face will be ?

A. Same in all three faces
B. Maximum in P position
C. Maximum in Q position
D. Maximum in R position

Answer 1

Hint:In the case, when a problem is based on the mechanical properties of a solid, we know that the Modulus of Rigidity plays a significant role in establishing a relationship between shear stress and shear strain hence, apply the formula of modulus of rigidity in the given problem in order to provide an accurate solution.

Formula used:
The formula of Modulus of Rigidity is,
$\text{Modulus of Rigidity}(\eta ) = \dfrac{\text{Shear Stress}({\sigma _s})}{\text{Shear Strain}(\theta )}$
The formula of shear stress is,
$\text{Shear Stress}({\sigma _s}) = \dfrac{\text{Force}}{\text{Area}}$
The formula of shear strain is,
$\text{Shear Strain}( \theta ) = \dfrac{{\Delta x}}{l}$

Complete step by step solution:
We know that $\text{Modulus of Rigidity}(\eta ) = \dfrac{\text{Shear Stress}({\sigma _s})}{\text{Shear Strain}(\theta )}$ … (1)
But $\text{Shear Stress}({\sigma _s}) = \dfrac{\text{Force}}{\text{Area}} = \dfrac{F}{A}$ and $\text{Shear Strain}(\theta ) = \dfrac{{\Delta x}}{l}$
From eq. (1), we get
$ \Rightarrow \eta = \dfrac{{\dfrac{F}{A}}}{{\dfrac{{\Delta x}}{l}}} = \dfrac{{F.l}}{{A.\Delta x}}$
Or, it can also be written as: -
$ \Rightarrow \Delta x = \dfrac{F}{\eta }.\dfrac{l}{A}$
Now if F and $\eta $ are constant, then $\Delta x$ varies with $\dfrac{l}{A}$

$ \Rightarrow \Delta x = \left( k \right)\dfrac{l}{A}$.......$\left( {Let,k = \dfrac{F}{\eta }} \right)$
Let us consider all the three cases given one by one: -
At position P, $\Delta x = \left( k \right)\dfrac{5}{{10 \times 8}} = \dfrac{{5k}}{{80}}$
At position Q, $\Delta x = \left( k \right)\dfrac{{10}}{{5 \times 8}} = \dfrac{{10k}}{{40}}$
At position R, $\Delta x = \left( k \right)\dfrac{8}{{10 \times 5}} = \dfrac{{8k}}{{50}}$
Clearly, it can be seen that the displacement to the upper face will be maximum in Q position rather than P and R. Thus, the displacement to the upper face will be maximum in Q position.

Hence, the correct option is C.

Note:Since this is a problem related to stress-strain analysis in mechanics hence, given conditions are analyzed very carefully, and quantities that are required to find the maximum displacement, such as shear modulus must be identified on a prior basis as it gives a better understanding of the problem.