Question

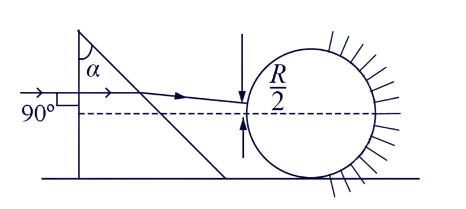
A ray in incident normally on a right-angle prism whose refractive index is √3 and prism angle α=30°. After crossing the prism, the ray passes through a glass sphere. It strikes the glass sphere of the same refractive index at a distance $\dfrac{R}{\sqrt{3}}$ from the principal axis, as shown in the figure. The net angle of deviation of the incident ray is ?

Answer 1

Hint: In this question we will use the concept of deviation in the path of a ray due to refraction while travelling from a denser to a rarer medium and vice versa. We will also be using the properties of reflection from a polished surface.

Complete step by step solution:
The incident ray is parallel strikes normally on a right-angle prism. Therefore, there will be no deviation on the first surface and the ray will pass and hit the second surface of the prism. At the second surface, the ray is travelling from a denser medium to a rarer medium.

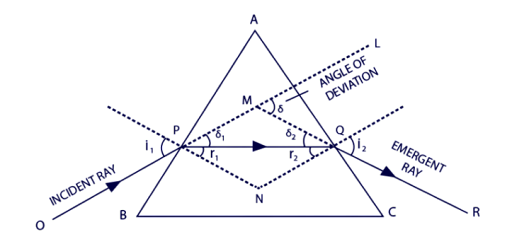
For any given triangle,
By geometry, $r_1+r_2$=angle of the triangle
In this question, $r_1$=0°, $r_2$= α=30°.
The relation between i, $r_1$ and μ (refractive index) is:
\[\mu =\dfrac{\sin (i)}{\sin (r)}\]
\[\Rightarrow \sqrt{3}=\]$\dfrac{\sin (i)}{\sin ({{30}^{\circ }})}$
Angle of emergence =60°
We know, angle of the triangle + deviation = i+e
Deviation = 0° + 60° - 30° = 30°

Now, the emergent ray hits the sphere at $\dfrac{R}{\sqrt{3}}$ distance from the principal axis. Making a triangle by dropping a perpendicular at the principal axis from the point where emergent ray hits the sphere. By geometry, we will get the angle opposite the side with height $\dfrac{R}{\sqrt{3}}$ = 30°. Therefore,
$\tan ({{30}^{\circ }})=\dfrac{\dfrac{R}{\sqrt{3}}}{base} \\ $
$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{R}{\sqrt{3}\times base} \\ $
$\Rightarrow base=R$

Since the value of the base is equal to radius, it implies that the ray was incident normally on the sphere surface and it passes through the centre of curvature of the sphere. Now, the ray passing through the centre of curvature of the sphere will hit the polished surface of the sphere normally. Hence, the ray will take a 180° turn and retrace its whole path.

Therefore, the net angle of deviation of the incident ray is 180°.

Note: On a polished surface, if the angle with normal is 0°, the ray will retrace its previous path. If an incident ray strikes normally on a right-angle prism, there will be no deviation on the surface and the ray will pass undeviated. A ray travelling from a denser medium to a rarer medium will bend away from the normal and not towards it.