Question

A progressive sound wave of frequency \[500Hz\] is travelling through air with a speed of $350m{s^{ - 1}}.$ A compression maximum appears at a place at a given instant. The minimum time interval after which the rarefaction maximum occurs at the same point, is:
A) $200s$
B) $\dfrac{1}{{250}}s$
C) $\dfrac{1}{{500}}s$
D) $\dfrac{1}{{1000}}s$

Answer 1

Hint: To solve this question, first, we need to find the time period of the sound wave and then assume the time interval between the rarefaction and the compression will be the minimum time interval after which the rarefaction maximum occurs at the same point at which the compression took place.

Complete step by step answer:
Let’s define all the terms given in the question:
Frequency of the sound wave, \[f = 500Hz\]
Speed of the sound wave, $v = 350m{s^{ - 1}}.$
The sound wave creates compression and rarefaction on the medium through which it propagates. The compression and rarefaction occurs alternatively.
In the compression region, the medium will be in a compressed form and in the portion of rarefaction, the medium will have a spread out form. The position of the particles do note change but vibrates, and the wave travels from one position to another.

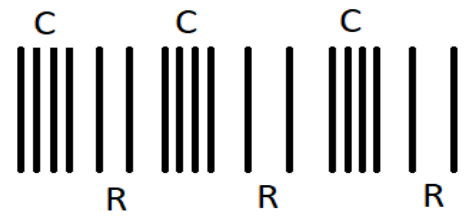
We know the time taken for a compression to compression ($C \to C$ in the figure) and rarefaction to rarefaction ($R \to R$ in the figure) is the same and which is taken as $T$
The period of the wave, $T = \dfrac{1}{f} = \dfrac{1}{{500}}$
The minimum time interval after which the rarefaction maximum occurs at the point at which the compression maximum ($C \to R$ in the figure) will be equal to
$\dfrac{T}{2} = \dfrac{{\left( {\dfrac{1}{{500}}} \right)}}{2}$
$ \Rightarrow \dfrac{1}{{500 \times 2}} = \dfrac{1}{{1000}}s$
The minimum time interval after which the rarefaction maximum occurs at the same point at which the compression took place, is
$\dfrac{1}{{1000}}s$

The final answer is option (D), $\dfrac{1}{{1000}}s$.

Note: Sound needs a medium for their propagation like solid or fluid to travel because the molecules of solid or fluid carry sound waves from one point to another. Sound cannot progress through vacuum because the vacuum does not have molecules which can vibrate and carry the sound waves.