
A point mass starts moving in a straight line with constant acceleration "a". At a time t after the beginning of motion, the acceleration changes sign, without change in magnitude. Determine the time \[{t_0}\] from the beginning of the motion in which the point mass returns to the initial position.
A. \[\left( {2 + \sqrt 3 } \right)t\]
B. \[\left( {2 + \sqrt 2 } \right)t\]
C. \[\left( {3 + \sqrt 2 } \right)t\]
D. \[\left( {12 + \sqrt 2 } \right)t\]
Answer
219k+ views
Hint:Point mass is moving with constant acceleration and after time t it will have negative acceleration, to find the total time for the mass in which it returns to initial point. We have to first calculate the time duration between the different points from beginning to end, then add it to get the total time \[{t_0}\].
Formula used :
The expression of equations of motion are,
$v = u + at$
And, \[{v^2} = {u^2} + 2as\]
Complete step by step solution:
Let the body start moving from a point A with acceleration a and initial velocity u and after time t at point B the acceleration changes sign and velocity is v but the acceleration will not be zero and as a result body will still move further in the straight path. After time $t_1$ at point C it will have final velocity v = o and will start moving backward to the initial point A.
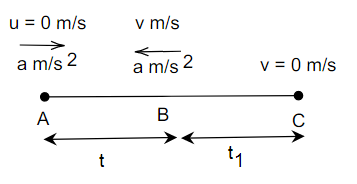
For length AB
$v = u + at$
$\Rightarrow v = 0 + at = at$ m/s
And,
\[{v^2} = {u^2} + 2as\\
\Rightarrow a{t^2} = 0 + 2a(AB)\\
\Rightarrow AB = \dfrac{{a{t^2}}}{2}\]
For length BC
$v = u+ at$
\[\Rightarrow 0 = at - a{t_1} \\
\Rightarrow {t_1} = t\]
And,
\[{v^2} = {u^2} + 2as\\
\Rightarrow 0 = a{t^2} - 2a(BC)\\
\Rightarrow BC = \dfrac{{a{t^2}}}{2}\]
Now, the velocity of the body at point C is zero and it will return back to point A and the time taken is $t_2$. From C to A
\[S = ut + \dfrac{1}{2}a{t^2}\\
\Rightarrow \dfrac{{a{t^2}}}{2} + \dfrac{{a{t^2}}}{2} = 0 + \dfrac{1}{2}at_2^2\\
\Rightarrow a{t^2} = \dfrac{{at_2^2}}{2} \\
\Rightarrow {t_2} = \sqrt 2 t\]
Therefore total time from the beginning in which the point mass returns to initial position will be,
\[{t_0} = t + {t_1} + {t_2} \\
\Rightarrow {t_0} = t + t + \sqrt 2 t \\
\Rightarrow {t_0} = \,2t + \sqrt 2 t \\
\therefore {t_0} = \left( {2 + \sqrt 2 } \right)t\]
Hence, for point mass to start from the beginning and then return to the initial point it will take time \[\left( {2 + \sqrt 2 } \right)t\].
Therefore, option B is the correct answer.
Note: One of the limitations of Newton’s Equation of mechanics is that they are not applicable for bodies having speed near speed of light. Moreover, equations of motion in physics are equations that explain how a physical system behaves in terms of how its motion changes over time. The behaviour of a physical system is described in further detail by the equations of motion as a collection of mathematical functions expressed in terms of dynamic variables. These variables typically consist of space, time, and sometimes elements of momentum.
Formula used :
The expression of equations of motion are,
$v = u + at$
And, \[{v^2} = {u^2} + 2as\]
Complete step by step solution:
Let the body start moving from a point A with acceleration a and initial velocity u and after time t at point B the acceleration changes sign and velocity is v but the acceleration will not be zero and as a result body will still move further in the straight path. After time $t_1$ at point C it will have final velocity v = o and will start moving backward to the initial point A.

For length AB
$v = u + at$
$\Rightarrow v = 0 + at = at$ m/s
And,
\[{v^2} = {u^2} + 2as\\
\Rightarrow a{t^2} = 0 + 2a(AB)\\
\Rightarrow AB = \dfrac{{a{t^2}}}{2}\]
For length BC
$v = u+ at$
\[\Rightarrow 0 = at - a{t_1} \\
\Rightarrow {t_1} = t\]
And,
\[{v^2} = {u^2} + 2as\\
\Rightarrow 0 = a{t^2} - 2a(BC)\\
\Rightarrow BC = \dfrac{{a{t^2}}}{2}\]
Now, the velocity of the body at point C is zero and it will return back to point A and the time taken is $t_2$. From C to A
\[S = ut + \dfrac{1}{2}a{t^2}\\
\Rightarrow \dfrac{{a{t^2}}}{2} + \dfrac{{a{t^2}}}{2} = 0 + \dfrac{1}{2}at_2^2\\
\Rightarrow a{t^2} = \dfrac{{at_2^2}}{2} \\
\Rightarrow {t_2} = \sqrt 2 t\]
Therefore total time from the beginning in which the point mass returns to initial position will be,
\[{t_0} = t + {t_1} + {t_2} \\
\Rightarrow {t_0} = t + t + \sqrt 2 t \\
\Rightarrow {t_0} = \,2t + \sqrt 2 t \\
\therefore {t_0} = \left( {2 + \sqrt 2 } \right)t\]
Hence, for point mass to start from the beginning and then return to the initial point it will take time \[\left( {2 + \sqrt 2 } \right)t\].
Therefore, option B is the correct answer.
Note: One of the limitations of Newton’s Equation of mechanics is that they are not applicable for bodies having speed near speed of light. Moreover, equations of motion in physics are equations that explain how a physical system behaves in terms of how its motion changes over time. The behaviour of a physical system is described in further detail by the equations of motion as a collection of mathematical functions expressed in terms of dynamic variables. These variables typically consist of space, time, and sometimes elements of momentum.
Recently Updated Pages
Two discs which are rotating about their respective class 11 physics JEE_Main

A ladder rests against a frictionless vertical wall class 11 physics JEE_Main

Two simple pendulums of lengths 1 m and 16 m respectively class 11 physics JEE_Main

The slopes of isothermal and adiabatic curves are related class 11 physics JEE_Main

A trolly falling freely on an inclined plane as shown class 11 physics JEE_Main

The masses M1 and M2M2 M1 are released from rest Using class 11 physics JEE_Main

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Understanding Uniform Acceleration in Physics

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

Understanding Atomic Structure for Beginners




