Question

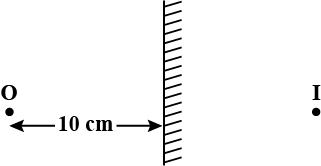
A plane mirror forms image I of an object O kept 10 cm from the mirror. It is found that when a Plano concave thin lens is placed in front of and in contact with the mirror (plane surface of the lens in contact with mirror), the position of the image formed by the plane mirror does not change. Then the refractive index of lens and radius of curvature of its curved surface are respectively'

A) $1.5,$ $10 cm$
B) $2.5,$ $10 cm$
C) $\sqrt 2 $, $10 cm$
D) $\text{All of these are possible}$

Answer 1

Hint: An image is defined as the collection of focus points of light rays coming from the object. The Refractive Index is defined as the ratio of the speed of light in a vacuum to its speed in a specific medium. The concave lenses are best for light projection and beam expansion.

Complete step by step solution:
When the object is placed at the center of the curvature, we know that from the laws of refraction, the image will be formed at the same distance as that of the object from the optical center. Thus we can conclude that the objects must be placed at the center of the curvature of the concave lens and the refractive index of the lens is not considered.

Hence the correct option is D.

Note: 1) If the refractive index increases, the thickness of the lens decreases thus resulting in less weight. The Refractive index is independent of the angle of incidence. Optical polymers that have a high refractive index will allow the light rays to bend more within the material.
2) The radius of curvature of the lens is defined as the radius of the hollow sphere of the glass of which the lens is a part. Each lens will have two radii of curvature. And also the focal length of the lens is inversely proportional to the refractive index of the material of medium.
3) The radius of curvature is positive, when the vertex lies to the left of the center of curvature and the radius of curvature is negative, when the vertex lies to the right of the center of curvature.