
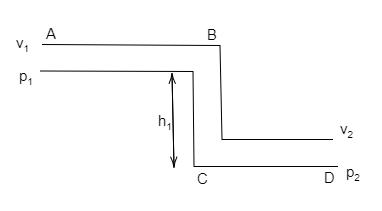
A pipe $ABCD$ of uniform cross-section is bent into three sections, viz. a horizontal section $AB$, a vertical section $BC$ with $C$ below $B$, and a horizontal section $CD$. Liquid flowing through the pipe has speed ${v_1}$ and pressure ${p_1}$ in section $AB$, and speed ${v_2}$ and pressure ${p_2}$ in section $CD$. Determine the relation between ${v_1}$ and ${v_2}$ ; ${p_1}$ and ${p_2}$?
(A) ${v_1} = {v_2}$, ${p_1} = {p_2}$
(B) ${v_1} = {v_2}$, ${p_2} > {p_1}$
(C) ${v_2} > {v_1}$, ${p_2} > {p_1}$
(D) ${v_2} > {v_1}$, ${p_1} = {p_2}$
Answer
232.8k+ views
Hint: The relation between the two velocities and pressure can be determined by the help of Bernoulli’s equation in fluid mechanics. By equating the input equation with the output equation, the relation between the two velocities and the two pressures can be determined.
Complete step by step answer:
Useful formula:
Bernoulli’s principle,
$\dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} + {p_1} = \dfrac{1}{2}\rho {v_2}^2 + \rho g{h_2} + {p_2}$
Where, $\rho $ is the density of the liquid flowing in the tube, $g$ is the acceleration due to gravity, ${h_1}$ is the elevation of the tube $AB$, ${h_2}$ is the elevation of the tube $CD$, ${v_1}$ is the velocity of the liquid flowing in the tube at input, ${v_2}$ is the velocity of the liquid flowing in the tube at output,
${p_1}$ is the pressure of the liquid flowing in the tube at input, ${p_2}$ is the pressure of the liquid flowing in the tube at output.
Complete step by step solution:
By Bernoulli’s principle, the total energy of the fluid flowing in the tube is equal to the sum of the potential energy, kinetic energy and the pressure energy.
By Bernoulli’s equation,
$\dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} + {p_1} = \dfrac{1}{2}\rho {v_2}^2 + \rho g{h_2} + {p_2}\,................\left( 1 \right)$
Here the fluid is flowing from top to bottom, so the elevation of the tube $CD$ is assumed to be zero, then the above equation is written as,
$\dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} + {p_1} = \dfrac{1}{2}\rho {v_2}^2 + \rho g\left( 0 \right) + {p_2}$
On multiplying the terms, then the above is,
$\dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} + {p_1} = \dfrac{1}{2}\rho {v_2}^2 + {p_2}$
By taking the density outside from the above equation on both sides, then the above equation is written as,
$\rho \left( {\dfrac{{{v_1}^2}}{2} + g{h_1} + \dfrac{{{p_1}}}{\rho }} \right) = \rho \left( {\dfrac{{{v_2}^2}}{2} + \dfrac{{{p_2}}}{\rho }} \right)$
By cancelling the term density on both sides, then the above equation is,
$\dfrac{{{v_1}^2}}{2} + g{h_1} + \dfrac{{{p_1}}}{\rho } = \dfrac{{{v_2}^2}}{2} + \dfrac{{{p_2}}}{\rho }$
Here the area of the pipe is constant, then there is no change in velocity, then assume that ${v_1} = {v_2}$, then the above equation is written as,
$\dfrac{{{v_1}^2}}{2} + g{h_1} + \dfrac{{{p_1}}}{\rho } = \dfrac{{{v_1}^2}}{2} + \dfrac{{{p_2}}}{\rho }$
By cancelling the same velocity terms on both sides, then the above equation is,
$g{h_1} + \dfrac{{{p_1}}}{\rho } = \dfrac{{{p_2}}}{\rho }$
By rearranging the terms for further calculation, then,
$g{h_1} = \dfrac{{{p_2}}}{\rho } - \dfrac{{{p_1}}}{\rho }$
By taking the density common in the denominator,
$g{h_1} = \dfrac{1}{\rho }\left( {{p_2} - {p_1}} \right)$
The above equation is written as,
$\rho g{h_1} = {p_2} - {p_1}$
Here, there is a pressure difference which shows that the pressure ${p_2}$ is greater than the pressure ${p_1}$.
Hence, the option (B) is correct.
Note: If the area of the pipe is increased, then the velocity is decreased and if the area of the pipe is decreased, then the velocity is increased. But in this problem the area of the pipe is constant, then the velocity is constant. And there is some pressure difference between ${p_2}$ and ${p_1}$, so the pressure ${p_2}$ is greater than ${p_1}$.
Complete step by step answer:

Useful formula:
Bernoulli’s principle,
$\dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} + {p_1} = \dfrac{1}{2}\rho {v_2}^2 + \rho g{h_2} + {p_2}$
Where, $\rho $ is the density of the liquid flowing in the tube, $g$ is the acceleration due to gravity, ${h_1}$ is the elevation of the tube $AB$, ${h_2}$ is the elevation of the tube $CD$, ${v_1}$ is the velocity of the liquid flowing in the tube at input, ${v_2}$ is the velocity of the liquid flowing in the tube at output,
${p_1}$ is the pressure of the liquid flowing in the tube at input, ${p_2}$ is the pressure of the liquid flowing in the tube at output.
Complete step by step solution:
By Bernoulli’s principle, the total energy of the fluid flowing in the tube is equal to the sum of the potential energy, kinetic energy and the pressure energy.
By Bernoulli’s equation,
$\dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} + {p_1} = \dfrac{1}{2}\rho {v_2}^2 + \rho g{h_2} + {p_2}\,................\left( 1 \right)$
Here the fluid is flowing from top to bottom, so the elevation of the tube $CD$ is assumed to be zero, then the above equation is written as,
$\dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} + {p_1} = \dfrac{1}{2}\rho {v_2}^2 + \rho g\left( 0 \right) + {p_2}$
On multiplying the terms, then the above is,
$\dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} + {p_1} = \dfrac{1}{2}\rho {v_2}^2 + {p_2}$
By taking the density outside from the above equation on both sides, then the above equation is written as,
$\rho \left( {\dfrac{{{v_1}^2}}{2} + g{h_1} + \dfrac{{{p_1}}}{\rho }} \right) = \rho \left( {\dfrac{{{v_2}^2}}{2} + \dfrac{{{p_2}}}{\rho }} \right)$
By cancelling the term density on both sides, then the above equation is,
$\dfrac{{{v_1}^2}}{2} + g{h_1} + \dfrac{{{p_1}}}{\rho } = \dfrac{{{v_2}^2}}{2} + \dfrac{{{p_2}}}{\rho }$
Here the area of the pipe is constant, then there is no change in velocity, then assume that ${v_1} = {v_2}$, then the above equation is written as,
$\dfrac{{{v_1}^2}}{2} + g{h_1} + \dfrac{{{p_1}}}{\rho } = \dfrac{{{v_1}^2}}{2} + \dfrac{{{p_2}}}{\rho }$
By cancelling the same velocity terms on both sides, then the above equation is,
$g{h_1} + \dfrac{{{p_1}}}{\rho } = \dfrac{{{p_2}}}{\rho }$
By rearranging the terms for further calculation, then,
$g{h_1} = \dfrac{{{p_2}}}{\rho } - \dfrac{{{p_1}}}{\rho }$
By taking the density common in the denominator,
$g{h_1} = \dfrac{1}{\rho }\left( {{p_2} - {p_1}} \right)$
The above equation is written as,
$\rho g{h_1} = {p_2} - {p_1}$
Here, there is a pressure difference which shows that the pressure ${p_2}$ is greater than the pressure ${p_1}$.
Hence, the option (B) is correct.
Note: If the area of the pipe is increased, then the velocity is decreased and if the area of the pipe is decreased, then the velocity is increased. But in this problem the area of the pipe is constant, then the velocity is constant. And there is some pressure difference between ${p_2}$ and ${p_1}$, so the pressure ${p_2}$ is greater than ${p_1}$.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




