Question

A person standing on a spring balance inside a stationary lift measures $60Kg$ The weight of that person if the lift descends with uniform downward acceleration of $1.8m{s^{ - 2}}$ will be ___ $N$. $[g = 10m{s^{ - 2}}]$

Answer 1

Hint: In order to solve this question, we will first draw the free diagram of all the forces acting on the man when the lift descends downward and then will calculate the net acceleration acting on the man which will produce the net weight effect on the spring balance.

Complete step by step solution:
Let us draw the free diagram of man as

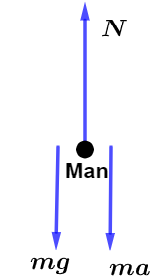
Image: Free body diagram of a man standing in a lift.

From the drawn free diagram of man, we can see that the normal reaction $N$ of the man which will be the reading of spring balance is in the upward direction, the original weight $mg$ is in the downward direction and man is also accelerating in the downward direction with an acceleration of $a = 1.8m{s^{ - 2}}$ which will produce a force in the downward direction with magnitude $ma$.

Now, mass of the man is given as $m = 60Kg$, $g = 10m{s^{ - 2}}$ and by balancing all the three forces we can write the equation as
$mg - N = ma$
On putting the values and solving for N we get,
$N = mg - ma$
$\Rightarrow N = m(g - a)$
$\Rightarrow N = 60(10 - 1.8)$
$\therefore N = 492\,N $

Hence, the reading of the spring balance will be $492\,N$.

Note: It should be remembered that mass and weight are two different things and here we were given the mass of the man as units of mass is Kg while weight is the downward force due to gravity and its unit is Newton. Always draw the free diagram of problems where forces and their directions are necessary to solve the problems.