
A part of a complete circuit is shown in the figure. At some instant, the value of current I is 1A and it is decreasing at a rate of \[{10^2}A{s^{ - 1}}\] . Then find the value of the potential difference \[{V_p} - {V_q}\], (in volts) at that instant.
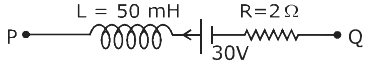
Answer
216k+ views
Hint:Application of Kirchoff's voltage will be there "In any closed-loop network, the total voltage surrounding the loop is equal to the sum of all the voltage drops within the same loop."
Formula used:
The expression of potential difference across the inductor is,
\[V = L\dfrac{{di}}{{dt}}\]
Where \[V = \] voltage and \[L = \] Inductance.
Complete step by step solution:
We know that
\[V = L\dfrac{{di}}{{dt}}\]
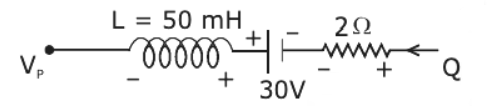
After applying the Kirchoff's voltage law in the above circuit we get;
\[{V_p} + L(\dfrac{{di}}{{dt}}) - 30 + 20i = {V_Q}\]
\[\Rightarrow {V_p} + 50({10^{ - 3}})({10^{ - 2}}) - 30 + 2 = {V_Q}\]
\[\Rightarrow {V_P} - {V_Q} = 35 - 2\]
\[\therefore {V_P} - {V_Q} = 33\]
Therefore, the value of the potential difference is 33.
Additional information: The unit of inductance in the SI system is the Henry (H), named after American scientist Joseph Henry, which is the amount of inductance which generates a voltage of one Volt when the current is changing at a rate of one Ampere per second.
Voltage: Voltage is the pressure from the power source of an electrical circuit that drives charged electrons (current) through a conducting loop, allowing them to perform tasks like lighting a lamp.
Note: While calculating the value of voltage drop across the inductor, the value should be converted into Henry for easy calculations. For the multiplication of exponential functions, power of these functions is always an additive process. e.g., If we take two exponential function \[{a^4}\] and \[{a^6}\] then the product of these two exponential functions is \[{a^4} \times {a^6} = {a^{4 + 6}} = {a^{10}}\], it should be give \[{a^4} \times {a^6} = {a^{4 \times 6}} = {a^{24}}\].
Formula used:
The expression of potential difference across the inductor is,
\[V = L\dfrac{{di}}{{dt}}\]
Where \[V = \] voltage and \[L = \] Inductance.
Complete step by step solution:
We know that
\[V = L\dfrac{{di}}{{dt}}\]
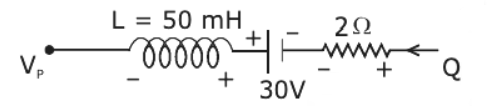
After applying the Kirchoff's voltage law in the above circuit we get;
\[{V_p} + L(\dfrac{{di}}{{dt}}) - 30 + 20i = {V_Q}\]
\[\Rightarrow {V_p} + 50({10^{ - 3}})({10^{ - 2}}) - 30 + 2 = {V_Q}\]
\[\Rightarrow {V_P} - {V_Q} = 35 - 2\]
\[\therefore {V_P} - {V_Q} = 33\]
Therefore, the value of the potential difference is 33.
Additional information: The unit of inductance in the SI system is the Henry (H), named after American scientist Joseph Henry, which is the amount of inductance which generates a voltage of one Volt when the current is changing at a rate of one Ampere per second.
Voltage: Voltage is the pressure from the power source of an electrical circuit that drives charged electrons (current) through a conducting loop, allowing them to perform tasks like lighting a lamp.
Note: While calculating the value of voltage drop across the inductor, the value should be converted into Henry for easy calculations. For the multiplication of exponential functions, power of these functions is always an additive process. e.g., If we take two exponential function \[{a^4}\] and \[{a^6}\] then the product of these two exponential functions is \[{a^4} \times {a^6} = {a^{4 + 6}} = {a^{10}}\], it should be give \[{a^4} \times {a^6} = {a^{4 \times 6}} = {a^{24}}\].
Recently Updated Pages
Wheatstone Bridge Explained: Working, Formula & Uses

Young’s Double Slit Experiment Derivation Explained

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

JEE Main Correction Window 2026 Session 1 Dates Announced - Edit Form Details, Dates and Link

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

How to Convert a Galvanometer into an Ammeter or Voltmeter

Atomic Structure: Definition, Models, and Examples

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance




