Question

A one-meter rod of mass 1.2kg is pivoted at one end and hangs vertically. It is displaced through an angle of 60 degrees. The increase in the potential energy is ( $g = 10m/{s^2}$ )
A) 1 joule
B) 1.5 joule
C) 3 joules
D) 6 joules

Answer 1

Hint: Potential energy is the energy held by an object because of its position relative to other objects. the mass of the rod is distributed all over the length of it. But we use the center of mass of the rod that is the midpoint of the rod because the resultant effect can be observed with the change in the center of mass. According to the question when the rod, pivoted at one end, is displaced at an angle of 60 degrees the center of mass will go upward. We can calculate the change in position of the center of mass by using Pythagoras theorem. Calculate potential energy in both the conditions and calculate the change.

Complete step by step solution:
Step 1: consider the following figure.

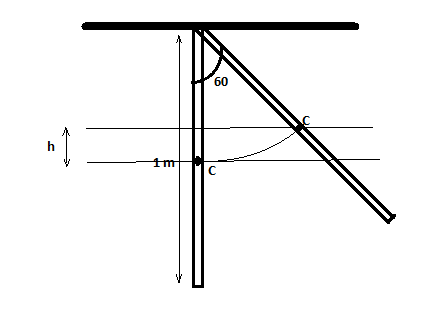
First, calculate the potential energy of the rod when it is pivoted at one end before displacing. Express the formula for the potential energy of the rod
\[\therefore {U_1} = mgh\]
Where $m$ is the mass of the rod, $g$ is the acceleration due to the gravitational force, $h$ is the height of the center of mass of the rod.
Take $h = \dfrac{l}{2} = \dfrac{1}{2}$ , $l = 1m$ is the length of the rod.
Step 2: substitute the values in the above formula
$\therefore {U_1} = 1.2 \times 10 \times \dfrac{1}{2}$
$ \Rightarrow {U_1} = 6.0joules$
Therefore, the PE of the rod is 6.0 joules.
Step 3: Now, when the rod is displaced 60 degrees, then the height $h = \dfrac{l}{2}\cos \theta $ will be the resultant height. Therefore, the potential energy of the rod is
$\therefore {U_2} = mg\dfrac{l}{2}\cos \theta $
Substitute the values in the above formula
$\therefore {U_2} = 1.2 \times 10 \times \dfrac{1}{2} \times \cos 60$
$ \Rightarrow {U_2} = 6 \times 0.5$
$ \Rightarrow {U_2} = 3.0joules$
Step 4: Now calculate the change in the potential energy.
$\therefore \Delta U = {U_1} - {U_2}$
$ \Rightarrow \Delta U = 6 - 3$
$ \Rightarrow \Delta U = 3joules$
Hence the potential energy will increase by 3 joules.

The correct answer is option C.

Note: The potential energy is directly proportional to the height of the object. More height means more energy is stored as potential energy. The potential energy will increase irrespective of the direction of displacement. Therefore, always remember the height of the center of mass increases then the PE of the body increases.