
A man of height h walks in a straight path towards a lamp post of height H with uniform velocity u. Then the velocity of the edge of the shadow on the ground will be
A. \[\dfrac{{Hu}}{{\left( {H - h} \right)}}\]
B. \[\dfrac{{Hu}}{{\left( {H + h} \right)}}\]
C. \[\dfrac{{H - h}}{{Hu}}\]
D. \[\dfrac{{H + h}}{{Hu}}\]
Answer
218.4k+ views
Hint:The light travels in a straight line and when an obstacle comes in the path of the light then it casts shadow. The distance of the edge of the shadow, the bottom of the lamp post and top of the lamp post makes a right angle triangle.
Formula used:
\[v = \dfrac{{dx}}{{dt}}\]
Here v is the velocity which is mathematically written as the rate of change of position.
Complete step by step solution:
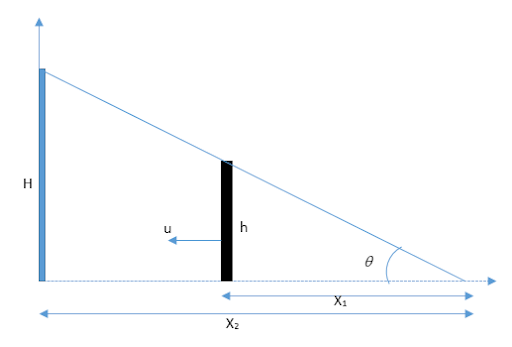
Image: Lamp post and man
Let at any instant of time, the length of the shadow is \[{x_2}\] and the distance of the edge of the shadow from the foot of the man is \[{x_1}\]. The height of the lamp post is given as H and the height of the man is given as h. The distance between the man and the lamp post will be,
\[x = {x_2} - {x_1}\]
It is given that the man is moving towards the lamp post at the uniform velocity u, i.e. the distance between the man and the lamp post is decreasing at the uniform rate of u.
As we know that the velocity is the rate of change of position,
\[ - u = \dfrac{{dx}}{{dt}}\]
\[\Rightarrow - u = \dfrac{{d\left( {{x_2} - {x_1}} \right)}}{{dt}}\]
\[\Rightarrow u = \dfrac{{d{x_1}}}{{dt}} - \dfrac{{d{x_2}}}{{dt}} \ldots \left( i \right)\]
Using congruence of triangle,
\[\tan \theta = \dfrac{H}{{{x_2}}} = \dfrac{h}{{{x_1}}}\]
\[\Rightarrow {x_1} = \dfrac{{h{x_2}}}{H}\]
On differentiating both the sides with respect to time, we get
\[\dfrac{{d{x_1}}}{{dt}} = \dfrac{h}{H}\left( {\dfrac{{d{x_2}}}{{dt}}} \right)\]
Here, \[\dfrac{{d{x_2}}}{{dt}}\] is the velocity of the edge of the shadow, let it be v
\[\dfrac{{d{x_1}}}{{dt}} = \dfrac{{hv}}{H}\]
Putting in the first equation, we get
\[u = \dfrac{{hv}}{H} - v\]
\[\Rightarrow u = v\left( {\dfrac{{h - H}}{H}} \right)\]
\[\therefore v = \dfrac{{Hu}}{{H - H}}\]
So, the edge of the shadow is moving on the ground with uniform speed \[\dfrac{{Hu}}{{H - h}}\].
Therefore, the correct option is A.
Note: Most of the students have confusion between the velocity and speed of an object. Always remember that velocity is a vector quantity and has both velocity and direction but speed is a scalar quantity and has only magnitude.
Formula used:
\[v = \dfrac{{dx}}{{dt}}\]
Here v is the velocity which is mathematically written as the rate of change of position.
Complete step by step solution:

Image: Lamp post and man
Let at any instant of time, the length of the shadow is \[{x_2}\] and the distance of the edge of the shadow from the foot of the man is \[{x_1}\]. The height of the lamp post is given as H and the height of the man is given as h. The distance between the man and the lamp post will be,
\[x = {x_2} - {x_1}\]
It is given that the man is moving towards the lamp post at the uniform velocity u, i.e. the distance between the man and the lamp post is decreasing at the uniform rate of u.
As we know that the velocity is the rate of change of position,
\[ - u = \dfrac{{dx}}{{dt}}\]
\[\Rightarrow - u = \dfrac{{d\left( {{x_2} - {x_1}} \right)}}{{dt}}\]
\[\Rightarrow u = \dfrac{{d{x_1}}}{{dt}} - \dfrac{{d{x_2}}}{{dt}} \ldots \left( i \right)\]
Using congruence of triangle,
\[\tan \theta = \dfrac{H}{{{x_2}}} = \dfrac{h}{{{x_1}}}\]
\[\Rightarrow {x_1} = \dfrac{{h{x_2}}}{H}\]
On differentiating both the sides with respect to time, we get
\[\dfrac{{d{x_1}}}{{dt}} = \dfrac{h}{H}\left( {\dfrac{{d{x_2}}}{{dt}}} \right)\]
Here, \[\dfrac{{d{x_2}}}{{dt}}\] is the velocity of the edge of the shadow, let it be v
\[\dfrac{{d{x_1}}}{{dt}} = \dfrac{{hv}}{H}\]
Putting in the first equation, we get
\[u = \dfrac{{hv}}{H} - v\]
\[\Rightarrow u = v\left( {\dfrac{{h - H}}{H}} \right)\]
\[\therefore v = \dfrac{{Hu}}{{H - H}}\]
So, the edge of the shadow is moving on the ground with uniform speed \[\dfrac{{Hu}}{{H - h}}\].
Therefore, the correct option is A.
Note: Most of the students have confusion between the velocity and speed of an object. Always remember that velocity is a vector quantity and has both velocity and direction but speed is a scalar quantity and has only magnitude.
Recently Updated Pages
Arithmetic, Geometric & Harmonic Progressions Explained

Cartesian Form of Vector Explained: Formula, Examples & Uses

Apparent Frequency Explained: Formula, Uses & Examples

Calorimetry: Definition, Principles & Calculations

Centrifugal Force Explained: Definition, Formula & Examples

Charge in a Magnetic Field: Definition, Formula & Examples

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

How to Convert a Galvanometer into an Ammeter or Voltmeter

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance

Understanding Average and RMS Value in Electrical Circuits




