Question

A magnetised wire of magnetic moment M and length l is bent in the form of a semicircle of radius r. The new magnetic moment is:

A) $M$
B) $\dfrac{{2M}}{\pi }$
C) $\dfrac{M}{\pi }$
D) None of the above

Answer 1

Hint: Since a magnet has two poles- North pole and the South pole. So the magnetic moment of a magnet is defined as the tendency of a magnet to get attracted towards a magnetic field. It is a vector quantity. It is the maximum torque experienced by a magnet when placed in an external magnetic field.

Complete step by step solution:
Step I: Suppose a bar magnet of length ‘l’ and magnetic moment ‘M’. Suppose that the bar magnet has a pole strength ‘m’, such that the magnetic moment is
$M = m.l$---(i)
The pole strength of the bar magnet is
$m = \dfrac{M}{l}$---(ii)

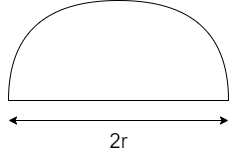
Step II: Now given that the bar magnet is bent in the form of a semicircle. The circumference of the semi circle is the length of the bar magnet which is equal to $l$.
Therefore, $l = \pi r$---(iii)

Step III: Given the length between the two poles of the magnet when it is bent into a semi circle is $2r$. Now the magnetic moment of the bent magnet is
$M' = m.(2r)$---(iv)
Substitute the value of ‘m’ from equation (ii) in equation (iv),
$M' = \dfrac{M}{l}.2r$
$M' = \dfrac{{2Mr}}{l}$

Step IV: Substitute the value of ‘l’ from equation (iii),
$M' = \dfrac{{2Mr}}{{\pi r}}$
$M' = \dfrac{{2M}}{\pi }$

Step V: The new magnetic moment is $\dfrac{{2M}}{\pi }.$

Therefore option B is the right answer.

Note: It is to be noted that there is another term used for magnetic moment. Sometimes it is also called magnetic dipole moment. The direction of magnetic moment points from the South pole to the North pole of the magnet. Magnetic dipoles align themselves in the direction of the external magnetic field.