Question

A ladder of mass M and length L is supported in equilibrium against a smooth vertical wall and a rough horizontal surface, as shown in figure. If $\theta $ be the angle of inclination of the rod with the horizontal, then calculate:

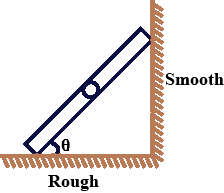
A) Normal reaction of the wall on the ladder.
B) Normal reaction of the ground on the ladder.
C) Net force applied by the ground on the ladder.

Answer 1

Hint: Here, we have been given with two surfaces, on the wall side the surface is smooth and on the ground side the surface is rough. The smooth surface indicates that there is no frictional force between the wall and the rod and the rough surface indicates that there is friction between the ground and the rod.

Complete step by step solution:
Resolve the forces in the x direction and y direction. See diagram below:

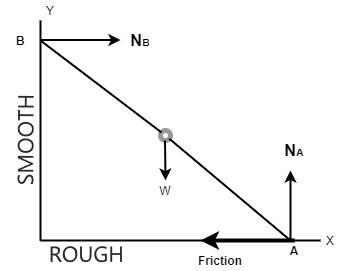
Now, the normal force is acting horizontally as well as vertically.
$\sum {{F_x} = 0;} $
Equate the horizontal forces:
$ \Rightarrow f - {N_B} = 0$;
$ \Rightarrow f = {N_B};$.........…(1)
Now, For the vertical forces:
$\sum {{F_y} = 0;} $
The vertical forces are:
$ \Rightarrow {N_A} - mg = 0$;
$ \Rightarrow {N_A} = mg$;............…(2)
Now, we would take torque about the center of rod:
Here, take the rod length L;
$\sum {{\tau _c} = 0;} $
$\left( {{N_A}} \right)\dfrac{L}{2}\cos \theta - \left( f \right)\dfrac{L}{2}\sin \theta - \left( {{N_B}} \right)\dfrac{L}{2}\sin \theta = 0$;.........…(3)
Put the value of $f = {N_B}$and ${N_A} = mg$in the above equation:
$\left( {mg} \right)\dfrac{L}{2}\cos \theta - \left( {{N_B}} \right)\dfrac{L}{2}\sin \theta - \left( {{N_B}} \right)\dfrac{L}{2}\sin \theta = 0$;
$ \Rightarrow \left( {mg} \right)\dfrac{L}{2}\cos \theta - \left( {{N_B}} \right)L\sin \theta = 0$;
Write in terms of the normal force:
$ \Rightarrow \left( {{N_B}} \right)L\sin \theta = \left( {mg} \right)\dfrac{L}{2}\cos \theta $;
\[ \Rightarrow \left( {{N_B}} \right) = \dfrac{{\left( {mg} \right)}}{2}\dfrac{{\cos \theta }}{{\sin \theta }}\];
Apply the necessary trigonometric property:
\[ \Rightarrow \left( {{N_B}} \right) = \dfrac{{\left( {mg} \right)}}{2}\dfrac{{\cos \theta }}{{\sin \theta }}\];
\[ \Rightarrow {N_B} = \dfrac{{mg}}{2}\cot \theta \];
Now for ${N_A}$:
We have the equation of torque:
$\left( {{N_A}} \right)\dfrac{L}{2}\cos \theta - \left( f \right)\dfrac{L}{2}\sin \theta - \left( {{N_B}} \right)\dfrac{L}{2}\sin \theta = 0$;
Put the value of ${N_B} = f$in the above equation:
$\left( {{N_A}} \right)\dfrac{L}{2}\cos \theta - \left( f \right)\dfrac{L}{2}\sin \theta - \left( f \right)\dfrac{L}{2}\sin \theta = 0$;
$ \Rightarrow \left( {{N_A}} \right)\dfrac{L}{2}\cos \theta - \left( f \right)L\sin \theta = 0$;
Do the necessary calculation:
$ \Rightarrow \dfrac{{\left( {{N_A}} \right)}}{2} = \left( f \right)\dfrac{{\sin \theta }}{{\cos \theta }}$;
$ \Rightarrow {N_A} = 2f\tan \theta $;
Now, calculate the net force:
${F_{net}} = \sqrt {{N_A} + f} $ ;
$ \Rightarrow {F_{net}} = \dfrac{1}{2}\sqrt {4 + {{\cot }^2}\theta } $;

Final answers are, Normal reaction of the wall on the ladder\[{N_B} = \dfrac{{mg}}{2}\cot \theta \]; Normal reaction of the ground on the ladder${N_A} = 2f\tan \theta $. Net force applied by the ground on the ladder ${F_{net}} = \dfrac{1}{2}\sqrt {4 + {{\cot }^2}\theta } $.

Note: Here, carefully construct a free body diagram mentioning all the forces that are given in the question. Then calculate all the horizontal net forces and net forces and since the body is in equilibrium the net horizontal and vertical forces are zero.