Question

A hemispherical portion of the radius $$R$$ is removed from the bottom of a cylinder of the radius $$R$$ . The volume of the remaining cylinder is $$V$$ and it's mass $$M$$ . It is suspended by a string in a liquid of density $$\rho$$ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is

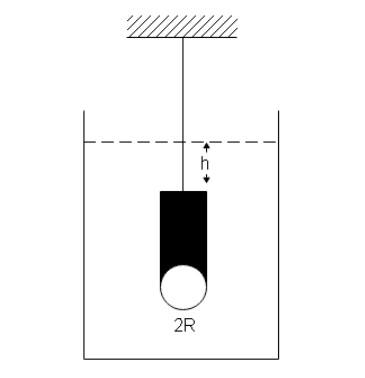
A) $Mg$
B) $Mg-\rho Vg$
C) $Mg+\pi R^{2}h\rho g$
D) $\rho g(V+\pi R^{2}h)$

Answer 1

Hint: The force in the bottom of the cylinder will be due to two different effects. There will be a buoyant force acting on the cylinder due to the water displaced by the cylinder. And there will be a force due to pressure on the cylinder due to the water above the cylinder.
Formula used: In this solution, we will use the following formula:
- Pressure due to height: $P=\rho gh$ where $\rho$ is the density of the fluid, $h$ is the depth of the liquid, and $g$ is the gravitational acceleration
- Buoyant force of an object: $F_b=\rho Vg$ where $\rho$ is the density of the fluid, $V$ is the volume, and $g$ is the gravitational acceleration

Complete step by step answer:
In the situation given to us, there will be two forces acting on the cylinder.
There will be an upward thrust on the cylinder. This is a result of buoyant force which arises because the cylinder has displaced water from the system. The magnitude of this force is calculated as
$F_b=\rho Vg$
Here we can directly calculate the buoyant force as we know the volume of the cylinder after removing the hemispherical section. The direction of this force will be in the upwards direction.
The second force that will be acting on the cylinder will be due to the mass of the water above the cylinder. The pressure of water above the cylinder due to height $h$ will be
$P=\rho gh$
Then the force on the cylinder can be calculated as a product of pressure and area as:
$F=P.A$
Since the area of the top surface of the cylinder is $\pi r^2$, the force will be
$F=\rho gh.\pi r^2$
This force will also be in the downwards direction but it will act at the top of the cylinder.
Hence we can balance the net force on the cylinder as
$F_{bottom}-F_{top}=\rho Vg$
Or
$F_{bottom}=F_{top}+\rho Vg$
Which gives us
$F_{bottom}=\rho Vg+\rho gh.\pi r^{2}g$
$\Rightarrow F_{bottom}=\rho g(V+\pi r^{2}h)$

Hence option (D) is the correct choice.

Note: Here we have assumed that the cylinder is incompressible. The reason the force on the top and the bottom of the cylinder will be different as the buoyant force will be acting on the bottom while the pressure of the water will be acting on the top of the cylinder.