Question

A disc of mass m and radius R is placed over a plank of mass m. There is sufficient friction between disc & plank to prevent slipping. A force F is applied at the centre of the disc then.


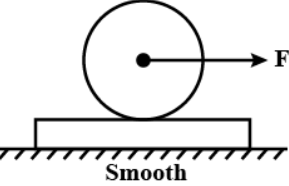
A. Acceleration of plank is $\dfrac{F}{{2m}}$
B. Acceleration of plank is $\dfrac{F}{{4m}}$
C. Friction force between disc and plank is $\dfrac{F}{7}$
D. Friction force between disc and plank is $\dfrac{F}{3}$

Answer 1

Hint:Here in this question, we have to know the fluctuation in velocity during a predetermined period of time. The average acceleration is calculated as the final velocity less the initial velocity divided by the time. ${A_{avg}} = \dfrac{{\Delta v}}{{\Delta t}}$ is the formula for average acceleration as a result.

Formula Used:
The formula of Torque,
$\tau = I\alpha $
Where, $I$ is the moment of inertia and $\alpha $ is the angular acceleration.

Complete step by step solution:
As we assume that the friction force will be f and the angular acceleration will be a. Now, we justify the accelerations of the disc as;
Acceleration of disc with respect to the centre is ${a_1}$.
And Acceleration of the disc with respect to the plank is ${a_2}$.
And we know that, the contact point through the torque will be equal to,
$\tau = I\alpha $
As from the diagram we get that,
$FR = \dfrac{{m{B^2}\alpha }}{2}.....(i)$
Similarly, we get that,
${a_1} - \alpha R = {a_2}$
As we know the value of ${a_2}$ by putting the value of ${a_2}$ in above equation, we get,
${a_1} - \alpha R = \dfrac{f}{m}$
Here from above equation, we need the value of ${a_1}$ , by rearranging we get that,
${a_1} = \dfrac{{3Ra}}{2}$

Now as accordance to force, the value is,
$\dfrac{F}{m} = 2aR$
As from the above equation, the value of a will be,
$\alpha = \dfrac{F}{{2mR}}$
As we get all values of ${a_1}$ and $\alpha $ now putting all in equation(i) to get the value of ${a_2}$ we get,
${a_2} = \dfrac{{R\alpha }}{2}$
Now by using, $\dfrac{F}{m} = 2aR$ in above equation, we get the resultant as,
${a_2} = \dfrac{F}{{4m}}$
Here we mentioned above that ${a_2}$ is the acceleration of plank. From which we get the acceleration of plank as ${a_2} = \dfrac{F}{{4m}}$. Therefore, the correct answer for Acceleration of plank is $\dfrac{F}{{4m}}$ .

Hence, the correct option is B.

Note: Rolling is maintained even as the body accelerates in rotation because friction moderates an increase in angular acceleration caused by net torque through a two-pronged action.