Question

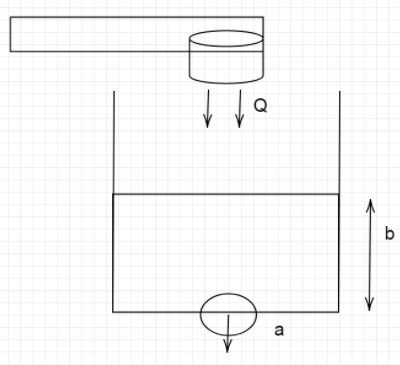
A cylindrical tank has a hole of $1{m^2}$ in its bottom. If the water is allowed to flow into the tank from a tube above it at the rate of $70c{m^3}/\sec $ then the maximum height up to which the water can rise in the tank is:

A) $2.5cm$
B) $5cm$
C) $10cm$
D) $0.25cm$

Answer 1

Hint: In the question, we need to calculate the maximum height attained by the liquid. It is evident that the height attained by the liquid must be maximum when the maximum volume of liquid flows through the hole.

Formula used:
$V = A\sqrt {2gh} $
where:
$V = $ Exit velocity
$A = $Area of the hole
$g = $Acceleration due to gravity
$h = $Height attained by the liquid.

Complete step by step solution:
In the question, we need an equation that relates to the speed of the fluid with the height attained by it.
We know, in fluid mechanics, Torricelli’s law relates the speed of the liquid exiting a hole with the height of the liquid. Torricelli’s law is applicable for ideal liquids.
In the question we have a similar scenario where we need to equate the rate at which the water flows through the hole to the rate at which water enters the tank:
Mathematically, the law can be written as:
$V = A\sqrt {2gh} $
where:
$V = $ Exit velocity
$A = $Area of the hole
$g = $Acceleration due to gravity
$h = $Height attained by the liquid.
Torricelli considered the liquid to be compressible, non-viscous, and have a laminar flow.
Now, we know for maximum height to be attained, the volume of water entering per second must equal the volume of water flowing out per second.
We can write:
The volume of water flowing in per second$ = 70c{m^3}/\sec $
Using Torricelli’s equation, the volume of water exiting $ = A\sqrt {2gh} $
Now, we obtain:
$\Rightarrow 70 = A\sqrt {2gh} $
We can write, area of the hole=$1{m^2} = 1 \times {10^4}c{m^2}$
Thus, putting the values, we arrive at:
$\Rightarrow 70 = 1 \times {10^4}\sqrt {2 \times 980 \times h} $
Therefore, on solving the equation, we get:
$\Rightarrow h = 25 \times {10^{ - 4}}cm$
This is our required solution.

Note: It is evident from the above equation of Torricelli’s equation, that the exit velocity is directly proportional to the height of the liquid obtained in the container. Thus, with an increase in height of the fluid within the container, the exit velocity also increases.