Question

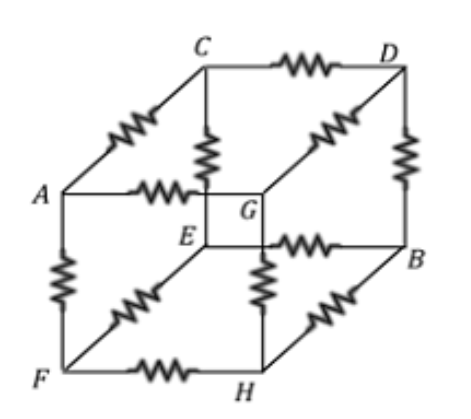
A cube made up of wire each of resistance R. Then find equivalent resistance across the diagonal.

a. $\dfrac{5}{6}R$
b. $\dfrac{3}{4}R$
c. $\dfrac{7}{12}R$
d. $R$

Answer 1

Hint: Here we have to find the equivalent resistance of the circuit in the shape of a cube. First of all, we have to simplify the circuit in order to find out the desired result. Here A and B is considered to be the ends or vertices which contain a diagonal.

Complete answer:
To find the equivalent resistance of the given circuit diagram in the shape of a cube. We have to simplify the cube in a $2$D sketch so that it is easily read or calculated.
Let us consider the diagonal to be AB.

So, we will formulate a sketch based on the $3$D structure of cube to a $2$D flat plane with A and B being the ends, as the question has asked to find out the resistance along a diagonal.
The sketch is formulated as:

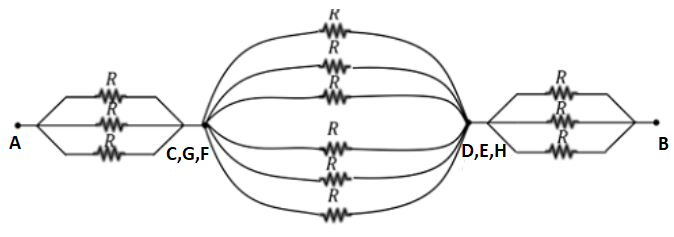
Due to symmetry, we have found out that the terminal C,G,F and D,E,H have the same potentials. So, can be regarded as the same point.

Now, the resistance around A and C,G,F are in parallel connection. Again, the resistance along B and D,E,H also the resistances along C,G,F and D,E,H are parallel. While all those three are in series connection.

So, the equivalent resistance is found as,
${{R}_{AB}}=\dfrac{R}{3}+\dfrac{R}{6}+\dfrac{R}{3}$
$\Rightarrow {{R}_{AB}}=\dfrac{5}{6}R$

The correct option is a. $\dfrac{5}{6}R$.

Note: It must be noted that we can figure out the equivalent resistance of anything in a $3$D format. So, our first aim must be to present it in the form of a $2$D sketch. And we must also remember that all the connections must be the same as that of a $3$D figure.