Question

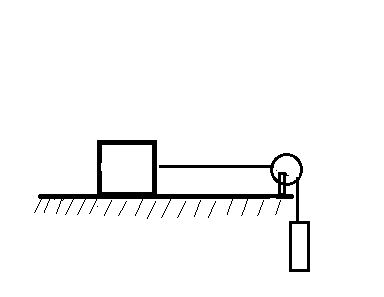
A constant force $F ={m_1}g/2$ is applied on the block of mass ${m_2}$ as shown in the figure. The string and pulley are light and the surface of the table is smooth. Find the acceleration of ${m_2}$.

Answer 1

Hint: Newton’s second law will be applied in this problem.
F = ma, force is equal to mass and acceleration; net force applied on an object because there are other forces also acting on an object such as frictional force, tension and gravitational force.

If net force is greater than other acting forces on the body acceleration in the body will take place.
Using the above mentioned concept we will calculate the acceleration of mass ${m_2}$.

Complete step by step solution:
Newton’s Second Law: It states that force is equal to the change in momentum and change in time.
$F = \dfrac{{dP}}{{dt}}$ (P is the momentum of the body)
Where P = m v (m is the mass of the body and v is the velocity of the body)
When change in velocity takes place acceleration is developed, therefore our equation becomes:
$F = \dfrac{{mdv}}{{dt}}$
$F = ma$

Let’s conclude the calculation part of the question now.
Force given to us, F = ${m_1}$g/2
Our equation becomes;
$ \Rightarrow T - F = {m_2}a$ (T is the tension of the string; F is the force we have applied)
$
   \Rightarrow {m_2}a = T - F \\
   \Rightarrow {m_2}a = T - \dfrac{{{m_1}g}}{2} \\
 $ (We have substituted the given value)....................(1)
Forces acting on mass ${m_1}$ are;
${m_1}a = {m_{1g}} - T$ ...........................(2)
On adding equation (1) and (2)
$
\Rightarrow {m_1}a + {m_2}a = T - \dfrac{{{m_1}g}}{2} + {m_1}g - T \\
\Rightarrow a({m_1} + {m_2}) = - \dfrac{{{m_1}g}}{2} + {m_1}g \\
$
(Cancelling the T on RHS and taking a common from LHS)

$\Rightarrow a({m_1} + {m_2}) = \dfrac{{ - {m_1}g + 2{m_1}g}}{2} \\
\Rightarrow a = \dfrac{{{m_1}g}}{{2\left( {{m_1} + {m_2}} \right)}} \\
$ (Acceleration of mass ${m_2}$)

Note: We have a number of daily life examples where we are observing Newton’s second law of motion such as, hitting the golf ball, cricket ball, football with a force the more we exert force the more we will observe the reaction. As in our question above force having higher magnitude was existing in the system.