Question

A concave mirror and a converging lens (glass with $\mu = 1.5$) both have a focal length of 3 cm when in air. When they are in water $\left( {\mu = \dfrac{4}{3}} \right)$ , their new focal lengths are:
A) ${f_{Lens}} = 12cm,{f_{Mirror}} = 3cm$
B) ${f_{Lens}} = 3cm,{f_{Mirror}} = 12cm$
C) ${f_{Lens}} = 3cm,{f_{Mirror}} = 3cm$
D) ${f_{Lens}} = 12cm,{f_{Mirror}} = 12cm$

Answer 1

Hint: In this question, we have to establish the relationship between the focal lengths of the mirror and lens and the refractive index of the material used for making them. However, the focal length of the mirror does not depend on the material but the focal length of the lens depends on the material and the medium it is present in.

Complete step by step answer:
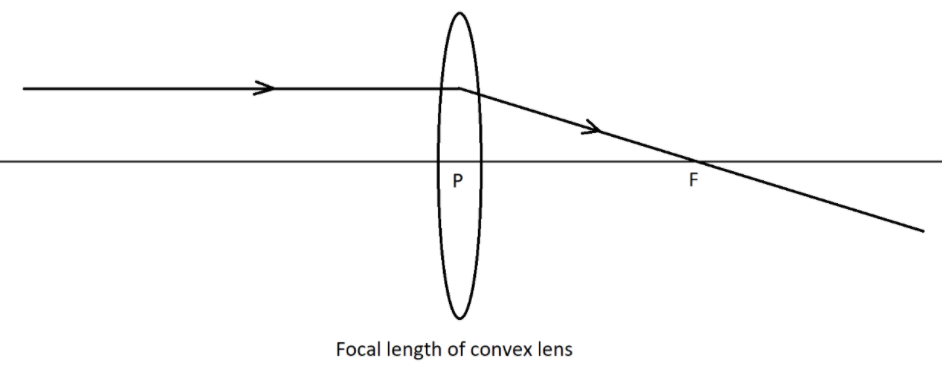
The focal point is defined as the point on the principal axis at which an incident ray from infinity, parallel to the principal axis of the mirror or lens, passes through this point.
The distance between the focal point of the mirror or lens from the pole is called focal length.


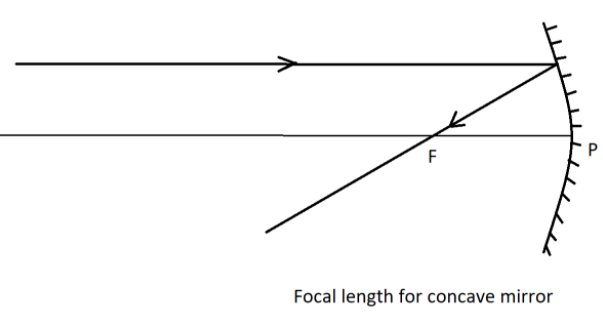
The formula used to calculate the focal length of concave or converging mirror is given by –
$\dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v}$
where u – distance of the object from pole and v – distance of the image from pole.
Here, we see that the focal length of the mirror does not depend on the medium it is present. Hence, if we place the mirror in any medium, the focal length remains the same.
Therefore, the focal length of the mirror is 3cm.
The formula used to calculate the focal length of the lens is given by the Lens Maker’s formula –
$f = \left( {{n_{21}} - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
where ${n_{21}} = \dfrac{{{n_2}}}{{{n_1}}}$= refractive index of the material of the lens with respect to the surrounding medium and ${R_1}\& {R_2}$ are the radii of curvature of the curved surfaces of the lens.
When the lens is in air, the focal length is equal to 3cm and refractive index, ${n_{21}} = \mu = 1.5$
Substituting,
$f = \left( {{n_{21}} - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
$\Rightarrow 3 = \left( {1.5 - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
$\Rightarrow \left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right) = \dfrac{3}{{0.5}} = 6$
When the lens is placed in the water, the refractive index ${n_2}$ changes to $\dfrac{4}{3}$ but the radii of curvature remain the same. The new focal length is –
$\Rightarrow f = \left( {{n_{21}} - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
The refractive index of glass with respect to water is given by –
$\Rightarrow {n_{21}} = \dfrac{{1.5}}{{\dfrac{4}{3}}}$
Substituting,
$\Rightarrow f = \left( {\dfrac{{4.5}}{4} - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
$ \Rightarrow f = \left( {\dfrac{{4.5 - 4}}{4}} \right) \times 6$
$ \Rightarrow f = \dfrac{{0.5}}{4} \times 6$
$ \Rightarrow f = 2 \times 6 = 12cm$
Therefore, when the convex lens is placed in the water, the focal length of the convex lens changes to 12cm.
Hence, the focal length of the mirror is 3cm and the focal length of the lens is 12cm.

The correct option is Option A.

Note: In the question it is given as a converging mirror. Concave mirror is a converging mirror because it converges a ray towards the focus. The convex mirror is a diverging mirror since it diverts the incoming ray away from the focus. But, in the spherical lens, the convex lens is the converging lens while the concave lens is the diverging lens. The students should be careful while considering convex or concave when it is given as diverging or converging.