Question

A circular hole of radius $\left( {\dfrac{a}{2}} \right)$ is cut out of a circular disc of radius ‘a’ shown in the figure. The centroid of the remaining circular portion with respect to point ‘O’ will be.
A. $\dfrac{{10a}}{{11}}$
B. $\dfrac{{2a}}{3}$
C. $\dfrac{a}{6}$
D. $\dfrac{{5a}}{6}$

Answer 1

Hint: Centroid is defined as the arithmetic means of all the points in the figure and it is also known as the center point of the given-on object. It always lies in the inside of an object.
In the question, we have a circle which is having a hole inside it and a radius $\left( {\dfrac{a}{2}} \right)$, it is
cut out from a circular disc. So, we have to use the centroid formula of the circle.

Formula used : The centroid is written as;
${X_{com}} = \dfrac{{{m_1}{x_1} - {m_2}{x_2}}}{{{m_1} - {m_2}}}$
Here, ${m_1}{\text{ and }}{m_2}$is the moment and ${x_1}{\text{ and }}{x_2}$ is the point.
For circle, $m = \sigma \pi {r^2}$
Where, $\sigma $ is the surface mass density of a disc.

Complete step by step solution:
To know about the distance between the circle along the x-axis and touch the y-axis let us find it with the help of the figure. The figure is shown below,

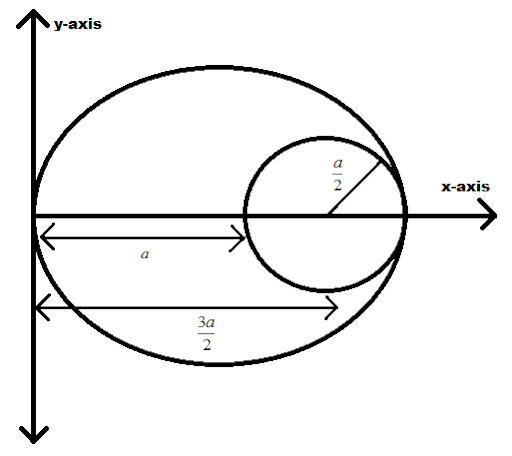
Here, as we see that the radius of the inner circle is $\left( {\dfrac{a}{2}} \right)$ and the outer circle radius is “a”, therefore it will be;
$a + \dfrac{a}{2} = \dfrac{{3a}}{2}$
Now we have the distance of two circles as “a” and “$\left( {\dfrac{{3a}}{2}} \right)$”.
Now, let us calculate the moment for the outer and the inner circles.
For the outer circle moment,${m_1}$ is written as;
${m_1} = \sigma \pi {a^2}$
For the inner circle, the moment is ${m_2}$;
${m_2} = \sigma \pi {\left( {\dfrac{a}{2}} \right)^2} \\
\Rightarrow {m_2} = \sigma \pi \dfrac{{{a^2}}}{4} \\ $
Now, putting these values in ${X_{com}} = \dfrac{{{m_1}{x_1} - {m_2}{x_2}}}{{{m_1} - {m_2}}}$ we have;
${X_{com}} = \dfrac{{(\sigma \pi {a^2})a - \left( {\sigma \pi \dfrac{{{a^2}}}{4}} \right)\left( {\dfrac{{3a}}{2}} \right)}}{{\sigma \pi {a^2} - \sigma \pi \dfrac{{{a^2}}}{4}}} \\
\Rightarrow {X_{com}} = \dfrac{{\sigma \pi {a^3} - \left( {\sigma \pi \dfrac{{3{a^3}}}{8}} \right)}}{{\dfrac{{4\sigma \pi {a^2} - \sigma \pi {a^2}}}{4}}} \\
\Rightarrow {X_{com}} = \dfrac{{\dfrac{{8\sigma \pi {a^3} - \left( {3\sigma \pi {a^3}} \right)}}{8}}}{{\dfrac{{4\sigma \pi {a^2} - \sigma \pi {a^2}}}{4}}} \\ $
Further solving,
$\Rightarrow {X_{com}} = \dfrac{{\dfrac{{5\sigma \pi {a^3}}}{8}}}{{\dfrac{{3\sigma \pi {a^2}}}{4}}} \\
\Rightarrow {X_{com}} = \dfrac{{5a}}{6} $

Hence, option D is correct

Note: The centroid is the center of the object and it is also called the center of gravity. It should always lie inside the object. The centroid is having a different surface mass density. According to the shape of the object surface density varies.