A circuit contains two capacitors in parallel wired in series to a resistor and source as shown above. The capacitors are initially uncharged. Which of the following describes the current I through and voltage $V_{c}$ across the Capacitor $C_{1}$ after the circuit reaches steady state?

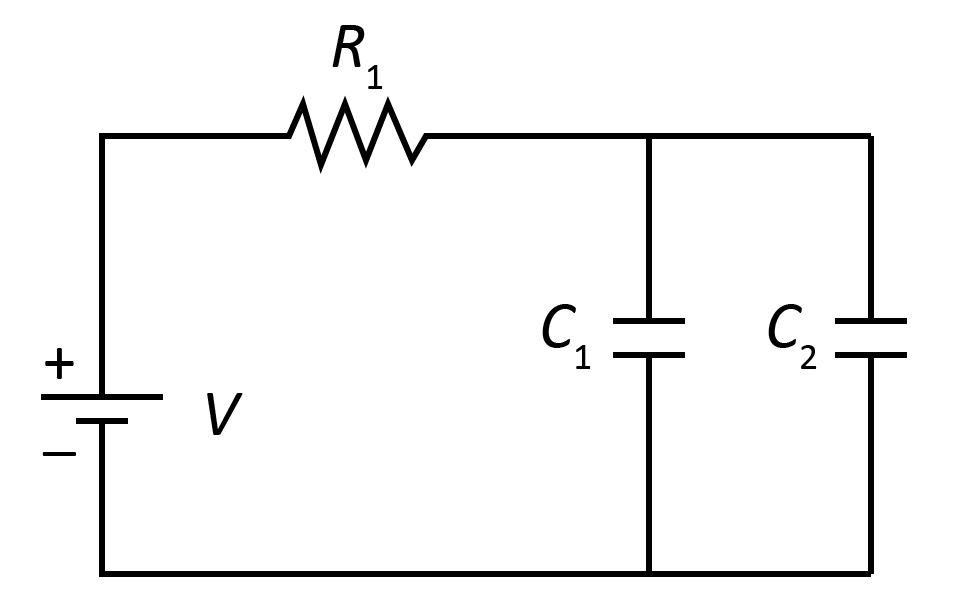
A) I=0 , $V_{c}$ =0
B) I=0, $V_{c}$ =V
C) I=0, $V_{c}$ =V/2
D) I=V/R, $V_{c}$ =0
E) I=V/R, $V_{c}$ =V

Answer

Verified

142.8k+ views

Hint: Experimentally the time taken for a capacitor to get completely charged is equal to t=RC where t is the time constant in charging of the capacitor in C-R circuit, R is the resistance of the resistor in series and C is the capacitance of the capacitor. From this we can conclude that adding a resistance in series will increase the time taken by the capacitor to get fully charged.

Complete step by step answer:
A capacitor is a charge storing device. It is connected to a resistor initially and charged through a battery. The charging process is time dependent and it takes some time depending on the RC value of the circuit for the capacitor to reach maximum charge. But since we are leaving the capacitor connected for a long time, we assume that it is storing its maximum charge.

A capacitor connected across a DC supply keeps on charging till the potential across the battery becomes equal to the potential difference across the capacitor. In steady state after some time the current in the circuit will numerically be equal to zero. Hence we will use Kirchhoff’s law of voltage to see in steady state the potential difference across the capacitor.

Therefore, I=0, $V_{c}$ =V and the correct option is (B).

Note: In an RC circuit, if the source is DC, the current then decreases from its initial value of I to zero as the voltage of the capacitor reaches the same value as the emf in case of transient period i.e. for a very short time in microseconds. As we know capacitors block the DC current, meaning the circuit will act as an open circuit.