Question

A circle is drawn to cut a chord of length 2a units X-axis and to touch the Y-axis. Find the locus of the center of the circle.
A.${x^2} + {y^2} = {a^2}$
B. ${x^2} - {y^2} = {a^2}$
C.$x + y = {a^2}$
D.${x^2} - {y^2} = 4{a^2}$

Answer 1

Hint: First draw a rough diagram to understand the given facts. Then suppose the coordinate of the center and apply Pythagoras theorem in the right-angle triangle of the diagram to obtain the required locus.

Formula Used:
Pythagoras theorem of right-angle triangle is,
${h^2} = {a^2} + {b^2}$ , where h is the hypotenuse, a is the height and b is the base.

Complete step by step solution:
The diagram of the given problem is,

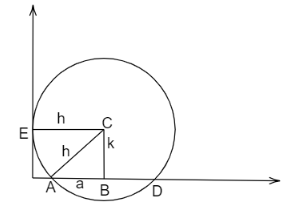
Image: Circle

Suppose that the coordinate of the circle is $C(h,k)$ .
We know that $AB = \dfrac{1}{2}AD$
Given that, $AD = 2a$ , therefore, $AB = a$ .
And, CE and CA are the radius of the circle, so the lengths are equal and equal to h.
Now, apply Pythagoras theorem in the right-angle triangle ABC,
${h^2} = {k^2} + {a^2}$
${h^2} - {k^2} = {a^2}$
Hence, the locus is,
${x^2} - {y^2} = {a^2}$

Option ‘B’ is correct

Note: The circle touches the y-axis, it means the abscissa of the center is the radius of the circle. The perpendicular from the center on a chord of a circle bisects the chord. Now apply Pythagorean theorem to find the locus of the center.