Question

A car is moving on a circular path and takes a turn. If ${R_1}$ and ${R_2}$ be the reactions on the inner and outer wheels respectively, then
A. ${R_1} = {R_2}$
B. ${R_1} < {R_2}$
C. ${R_1} > {R_2}$
D. ${R_1} \geqslant {R_2}$

Answer 1

Hint: In order to solve this question, we will first draw the rough diagram of wheels of the car and then indicate their normal reactions and then using concept of moment about the centre of gravity of the car we will determine the correct relation between normal reactions of the wheels.

Complete step by step solution:
According to the question, we have given that A car is moving on a circular path and takes a turn and in this ${R_1}$ and ${R_2}$ be the reactions on the inner and outer wheels, while turning the horizontal force required to make a turn is centripetal force f which is given by,
$f = \dfrac{{M{v^2}}}{r}$
where m is the mass, v is the velocity and r is the radius of the circular path.

Let us draw the free body diagram of wheels of the car where height of the wheel is h and distance between two wheels is $2a$ and G is the point of centre of gravity of the car as shown in the diagram


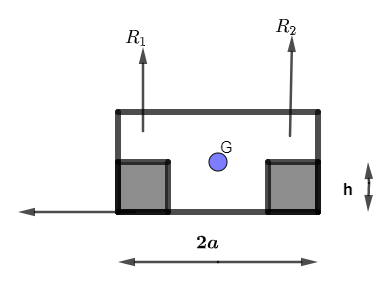
Now, if the car is turning towards left as shown in the diagram then on balancing vertical force we have,
${R_1} + {R_2} = Mg$
Now, taking the moments of vertical forces and horizontal forces about the point G, we get;
$Fh + {R_1}a = {R_2}a \\
\Rightarrow {R_2} = \dfrac{{Fh + {R_1}a}}{a} \\
\Rightarrow {R_2} = {R_1} + \dfrac{{Fh}}{a} \\ $
$\therefore {R_2} > {R_1}$

Hence, the correct answer is option B.

Note: It should be remembered that, if the car was taking the turn towards right then these reactions will be exactly opposite as horizontal centripetal force will act towards right and always make the free body diagram to solve such questions.