Question

A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of the resulting system:
$\left( a \right)$ Increase by a factor of $2$
$\left( b \right)$ Increase by a factor of $4$
$\left( c \right)$ Decrease by a factor of $2$
$\left( d \right)$ Remains the same

Answer 1

Hint: Kirchhoff’s Voltage Law is that the second of his elementary laws we will use for circuit analysis. His voltage law states that for a closed-loop system series path the algebraically total of all the voltages around any closed-loop system in an exceeding circuit is adequate zero. This is often as a result of a circuit loop that could be a closed conducting path thus no energy is lost.

Complete step by step solution: Here in the question it is given that the capacitor is charged initially with the battery. For this, the diagram is shown below.

                                               
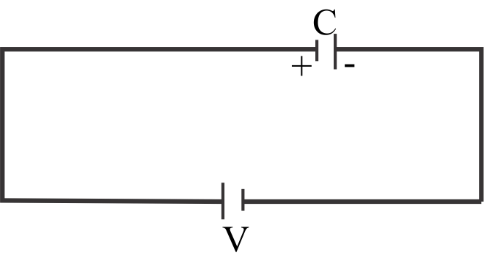
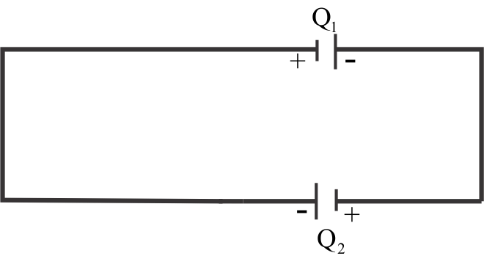
The total charge is equal to ${Q_0}$;
Therefore from the figure, we can write,
$ \Rightarrow {Q_1} + {Q_2} = {Q_0}$
Now applying KVL,
And as we know in KVL for a closed-loop system series path the algebraically total of all the voltages around any closed-loop system in an exceeding circuit is adequate zero.
Therefore,
\[ \Rightarrow \dfrac{{{Q_1}}}{C} = \dfrac{{{Q_2}}}{C} = 0\]
On further solving the equation, we can write it as;
$ \Rightarrow {Q_1} = {Q_2}$
And since ${Q_1} + {Q_2} = {Q_0}$
Therefore
$ \Rightarrow {Q_1} = {Q_2} = \dfrac{{{Q_0}}}{2}$
Since the initial electrostatic charge is,
\[ \Rightarrow {E_i} = \dfrac{1}{2}C{V^2} = \dfrac{{Q_0^2}}{{2C}}\]
Therefore, the final electrostatic charge will be
\[ \Rightarrow {E_f} = \dfrac{1}{2}C{V^2} + \dfrac{1}{2}C{V^2}\]
Now putting the values which we have calculated initially in the above equation, we get
\[ \Rightarrow \dfrac{{Q_1^2}}{{2C}} + \dfrac{{Q_2^2}}{{2C}}\]
On further solving,
\[ \Rightarrow \dfrac{{Q_0^2}}{{8C}} + \dfrac{{Q_0^2}}{{8C}}\]
Adding both the terms, we get
\[ \Rightarrow \dfrac{{Q_0^2}}{{4C}}\]
So now we will calculate the ratio of ${E_f}$and ${E_i}$
We get,
$\dfrac{{{E_f}}}{{{E_i}}} = \dfrac{{\dfrac{{Q_0^2}}{{4C}}}}{{\dfrac{{Q_0^2}}{{2C}}}}$
On solving this, we get
$\dfrac{{{E_f}}}{{{E_i}}} = \dfrac{1}{2}$

Therefore, the total electrostatic energy of the resulting system decrease by a factor $2$.

Note: The theory behind Kirchhoff’s second law is additionally called the law of conservation of voltage, and this is often notably helpful for us once managing series circuits, as series circuits conjointly act as voltage dividers and therefore the voltage divider circuit is a very important application of the many series circuits.