Question

A body of mass $\sqrt 3 \,kg$ is suspended by a string to rigid support. The body is pulled horizontally by a force $F$ until the string makes an angle of ${30^ \circ }$ with the vertical. The value of $F$ and tension in the string are:
(A) $9.8\,N$, $9.8\,N$
(B) $9.8\,N$, $19.6\,N$
(C) $19.6\,N$, $19.6\,N$
(D) $19.6\,N$, $9.8\,N$

Answer 1

Hint By using the given information the free body diagram is drawn, by using the information in the diagram the value of force and the value of the tension in the string can be determined. By taking the horizontal component, the value of force can be determined and by using the vertical component the tension of the string can be determined.

Complete step by step solution
Given that,
The mass of the body is, $m = \sqrt 3 \,kg$,
The angle of the string with respect to vertical is, $\theta = {30^ \circ }$,
So, the angle of the string with respect to the horizontal is, $\theta = {60^ \circ }$
By using the given information, the free body diagram is given by,


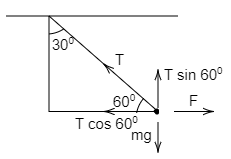
From the diagram shown above,
To determine the value of the tension on the string, then we use the vertical component of the object, then
$F = T\sin {60^ \circ }$
By substituting the value of the $\sin {60^ \circ }$ from the trigonometry in the above equation, then the above equation is written as,
$F = T \times \dfrac{{\sqrt 3 }}{2}$
Now the force in the above equation is written as,
$mg = T \times \dfrac{{\sqrt 3 }}{2}$
By substituting the mass of the object and the acceleration due to gravity in the above equation, then
$\sqrt 3 \times 9.8 = T \times \dfrac{{\sqrt 3 }}{2}$
By cancelling the same terms in the above equation, then the above equation is written as,
$9.8 = T \times \dfrac{1}{2}$
By rearranging the terms in the above equation, then
$T = 9.8 \times 2$
By multiplying the terms in the above equation, then
$T = 19.6\,N$
From the diagram shown above,
To determine the value of the force, then we use the horizontal component of the object, then
$F = T\cos {60^ \circ }$
By substituting the value of the $\cos {60^ \circ }$ from the trigonometry in the above equation, then the above equation is written as,
$F = T \times \dfrac{1}{2}$
By substituting the value of the tension of the string in the above equation, then
$F = 19.6 \times \dfrac{1}{2}$
By dividing the terms in the above equation, then
$F = 9.8\,N$

Hence, the option (B) is the correct answer.

Note The tension of the string is equated with the product of the mass of the object and the acceleration of the object because from the diagram opposite to the tension equation the component $mg$ is acting, so both are equated. Like that the force equation is equated with $F$ only.