Question

A bar magnet \[10cm\] long is kept with its north (N)-pole pointing north. A neutral point is formed at a distance of \[15cm\] from each pole. Given the horizontal component of the earth’s magnetic field is \[0.4Gauss\] , the pole strength of the magnet is
(A) \[9A-m\]
(B) \[6.75A-m\]
(C) \[27A-m\]
(D) \[1.35A-m\]

Answer 1

Hint: A neutral point is a point at which the resultant magnetic field is zero. In general, a neutral point is obtained when the magnetic field produced by the magnet balances the horizontal component of the earth’s field. We have been given the value of the earth’s horizontal magnetic field. If we find the magnetic field of the magnet and equate it to the earth’s magnetic field, we’ll find our answer.

Formula Used:
\[{{B}_{H}}=\dfrac{{{\mu }_{0}}}{2\pi }\times \dfrac{M}{{{({{d}^{2}}+{{t}^{2}})}^{\dfrac{3}{2}}}}\]

Complete step by step answer:
The neutral point is obtained on the line perpendicular to the magnet and passing through the midpoint of the magnet. We have been told the magnet’s length. The length of each pole will be half of this given length. You can visualize the arrangement with the help of the following image. Let the neutral point be O.

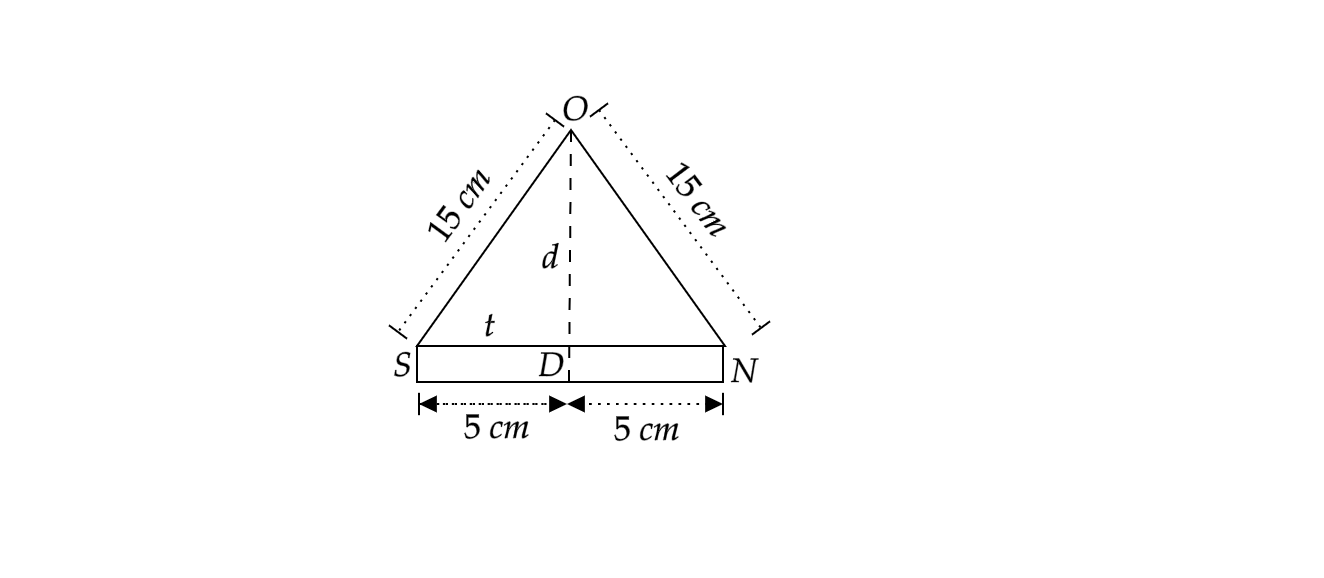
The magnetic field due to the magnet at the neutral point O will be equal to \[\dfrac{{{\mu }_{0}}}{2\pi }\times \dfrac{M}{{{({{d}^{2}}+{{t}^{2}})}^{\dfrac{3}{2}}}}\] where \[M\] is the magnetic pole strength of the magnet, \[d\] is marked in the diagram above and \[t\] is the length of each magnetic pole, which has also been shown in the diagram.
If we consider the triangle OSD in the diagram, we can say that \[\text{O}{{\text{S}}^{\text{2}}}=({{d}^{2}}+{{t}^{2}})\], using Pythagoras theorem.
Raising both the sides of the above expression to the power \[\dfrac{3}{2}\], we get \[\text{O}{{\text{S}}^{3}}={{({{d}^{2}}+{{t}^{2}})}^{\dfrac{3}{2}}}\]
Since we know the value of the side OS, we can say that
\[\begin{align}
  & {{({{d}^{2}}+{{t}^{2}})}^{\dfrac{3}{2}}}={{(15cm)}^{3}} \\
 & \Rightarrow {{({{d}^{2}}+{{t}^{2}})}^{\dfrac{3}{2}}}={{(15\times {{10}^{-2}}m)}^{3}}\left[ \because 1cm={{10}^{-2}}m \right] \\
 & \Rightarrow {{({{d}^{2}}+{{t}^{2}})}^{\dfrac{3}{2}}}=3375\times {{10}^{-6}}{{m}^{3}} \\
\end{align}\]
The value of the horizontal component of the earth’s magnetic field \[({{B}_{H}})=0.4G=0.4\times {{10}^{-4}}T\left[ \because 1\text{ Tesla = }{{10}^{-4}}\text{ Gauss} \right]\]
Substituting all the values in the expression \[{{B}_{H}}=\dfrac{{{\mu }_{0}}}{2\pi }\times \dfrac{M}{{{({{d}^{2}}+{{t}^{2}})}^{\dfrac{3}{2}}}}\] , we get
\[\begin{align}
  & 0.4\times {{10}^{-4}}={{10}^{-7}}\times \dfrac{M}{3375\times {{10}^{-6}}}\left[ \because \dfrac{{{\mu }_{0}}}{2\pi }={{10}^{-7}} \right] \\
 & \Rightarrow M=3375\times 0.4\times {{10}^{-3}} \\
 & \Rightarrow M=1.35A-m \\
\end{align}\]
Hence the correct option is (D).

Note: While calculating the magnetic field of the magnet, students often make an error. Instead of taking the value of the hypotenuse, which has already been given in the question, they apply the Pythagoras theorem and calculate the value of the perpendicular from the magnet to the neutral point as that is the only unknown value. You should avoid making such mistakes.